Hoạt động khám phá 2 trang 13 Toán lớp 6 Tập 2: Đưa hai phân số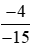 và
và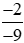 về dạng hai phân số có mẫu dương rồi quy đồng mẫu của chúng.
về dạng hai phân số có mẫu dương rồi quy đồng mẫu của chúng.
Câu hỏi trong đề: Giải SGK Toán 6 Chương 5: Phân số - Bộ Chân trời sáng tạo !!
Quảng cáo
Trả lời:
Lời giải:
- Đưa hai phân số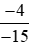 và
và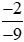 về cùng mẫu dương, ta được:
về cùng mẫu dương, ta được:
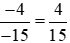 và
và 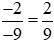 .
.
- Quy đồng mẫu số hai phân số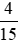 và
và , ta được:
, ta được:
Mẫu số chung: 45.
Ta thực hiện: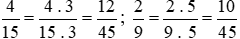 .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
Mẫu số chung của hai hay nhiều phân số là số chia hết cho tất cả các mẫu số của các phân số đó.
Ta thường để mẫu số chung là bội chung nhỏ nhất của các số ở mẫu để các phân số sau khi quy đồng sẽ đơn giản nhất có thể.
Ta có: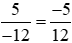
* Quy đồng hai phân số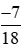 và
và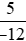 .
.
Mẫu số chung: 36.
Ta thực hiện: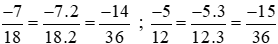 .
.
Vì –14 > –15 nên 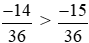
Do đó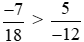 .
.
Vậy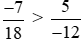 .
.
Lời giải
Lời giải:
a) Ta có: −2 =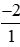 .
.
Mẫu số thích hợp để so sánh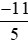 với
với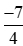 với –2 là mẫu số chung của ba phân số
với –2 là mẫu số chung của ba phân số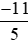 ;
;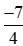 và −2 (ta nên tìm mẫu chung nhỏ nhất để phân số sau khi quy đồng đơn giản nhất có thể).
và −2 (ta nên tìm mẫu chung nhỏ nhất để phân số sau khi quy đồng đơn giản nhất có thể).
Mẫu số chung là 20.
Ta thực hiện:
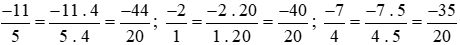
Vì −44 < −40 nên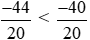 hay
hay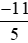 < −2.
< −2.
Vì −40 < −35 nên 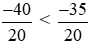 hay −2 <
hay −2 <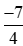 .
.
Áp dụng tính chất bắc cầu, ta suy ra: < .
Vậy 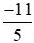 <
<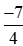 .
.
b) So sánh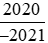 với
với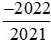 .
.
Nhận thấy: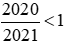 và
và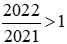 .
.
Do đó để so sánh hai phân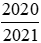 và
và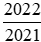 , ta có thể so sánh chúng với 1.
, ta có thể so sánh chúng với 1.
Suy ra ta có thể so sánh hai phân số 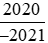 với
với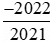 với −1.
với −1.
Cách 1: So sánh hai phân số trên với −1 và áp dunng tính chất bắc cầu.
Ta có: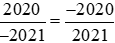
Vì 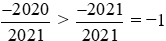
Và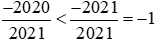
Do đó áp dụng tính chất bắc cầu, ta suy ra: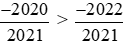 .
.
Vậy 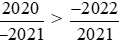 .
.
Cách 2: Đưa hai phân số về cùng mẫu dương rồi so sánh:
Ta có: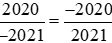 .
.
Vì −2020 > −2022 nên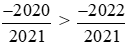 .
.
Vậy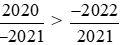 .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
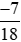 và
và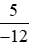 .
.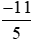 với
với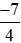 với –2 bằng cách viết –2 ở dạng phân số có mẫu số thích hợp. Từ đó suy ra kết quả so sánh
với –2 bằng cách viết –2 ở dạng phân số có mẫu số thích hợp. Từ đó suy ra kết quả so sánh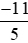 với
với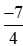 .
.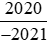 với
với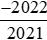 .
.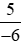 ;
;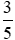 ; −1;
; −1;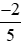 ; 0 theo thứ tự tăng dần.
; 0 theo thứ tự tăng dần.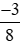 và
và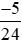 ;
;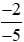 và
và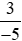 ;
;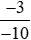 và
và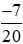 ;
;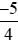 và
và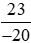 .
.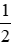 hoặc
hoặc thanh sô cô la đó. Theo em bạn Nam sẽ chọn phần nào?
thanh sô cô la đó. Theo em bạn Nam sẽ chọn phần nào?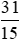 và 2;
và 2;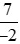 .
.