Câu hỏi trong đề: Giải SGK Toán 6 Chương 5: Phân số - Bộ Chân trời sáng tạo !!
Quảng cáo
Trả lời:
Lời giải:
Đây là phép trừ hai phân số, ta lấy phân số thứ nhất cộng với số đối của phân số thứ hai, rồi thực hiện cộng hai phân số như bình thường.
Ta thực hiện như sau: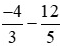
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
Để tách một phân số thành tổng của các phân số có tử số bằng 1 thì ta cần tách thỏa mãn:
- Các số sau khi tách ra thuộc ước của mẫu số.
- Tổng của hai hay nhiều số đó bằng tử số của phân số đã cho.
a) Phân số  ;
;
Các ước của mẫu là các số tự nhiên: Ư(3) = .
Nhận thấy: tổng của hai số thuộc ước tự nhiên của 3 không có tổng bằng 2.
Nên ta biến đổi: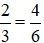 .
.
- Các ước của mẫu là các số tự nhiên: Ư(6) = .
- Các số khác nhau thuộc thuộc tập hợp Ư(6) là số tự nhiên và có tổng bằng 4 là 3 và 1.
Do đó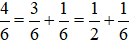
Vậy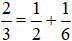 .
.
b) Phân số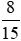 ;
;
- Các ước của mẫu là các số tự nhiên: Ư(15) = .
- Các số khác nhau thuộc thuộc tập hợp Ư(15) là số tự nhiên và có tổng bằng 8 là 5 và 3.
Do đó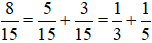
Vậy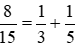 .
.
c) Phân số 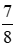 ;
;
- Các ước của mẫu là các số tự nhiên: Ư(8) = .
- Các số khác nhau thuộc thuộc tập hợp Ư(8) là số tự nhiên và có tổng bằng 7 là 4; 2 và 1.
Do đó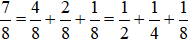
Vậy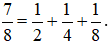
d) Phân số 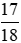 ;
;
- Các ước của mẫu là các số tự nhiên: Ư(18) = .
- Các số khác nhau thuộc thuộc tập hợp Ư(18) là số tự nhiên và có tổng bằng 17 là 9; 6 và 2.
Do đó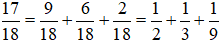
Vậy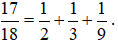
Lời giải
Lời giải:
Hai phân số đối nhau nếu tổng của chúng bằng 0.
a) Số đối của phân số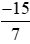 là phân số
là phân số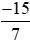 hay
hay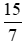 ,vì
,vì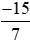 +
+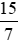 = 0;
= 0;
b) Số đối của phân số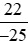 là phân số
là phân số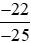 hay
hay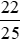 ,vì
,vì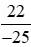 +
+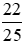 = 0;
= 0;
c) Số đối của phân số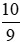 là phân số
là phân số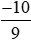 ,vì
,vì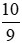 +
+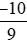 = 0;
= 0;
d) Số đối của phân số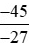 là
là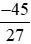 , vì
, vì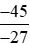 +
+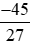 = 0.
= 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
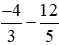 .
. ;
;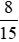 ;
;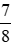 ;
;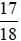 .
.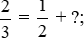
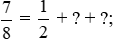
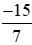 ;
;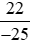 ;
;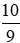 ;
; 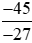 .
.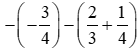 .
. quyển sách, ngày thứ hai đọc được
quyển sách, ngày thứ hai đọc được quyển sách, ngày thứ ba đọc được
quyển sách, ngày thứ ba đọc được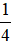 quyển sách. Hỏi hai ngày đầu Bảo đọc nhiều hơn hay ít hơn hai ngày sau? Tìm phân số để chỉ số chênh lệch đó.
quyển sách. Hỏi hai ngày đầu Bảo đọc nhiều hơn hay ít hơn hai ngày sau? Tìm phân số để chỉ số chênh lệch đó.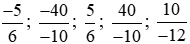
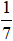 bể, vòi thứ hai mỗi giờ chảy được
bể, vòi thứ hai mỗi giờ chảy được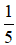 bể. Nếu mở đồng thời cả hai vòi, mỗi giờ được mấy phần bể?
bể. Nếu mở đồng thời cả hai vòi, mỗi giờ được mấy phần bể?