Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải:
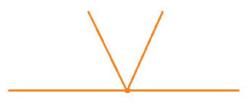
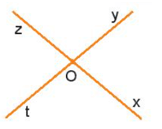
Đặt tên: đỉnh O và các tia Ox, Oy, Oz, Ot như hình vẽ.
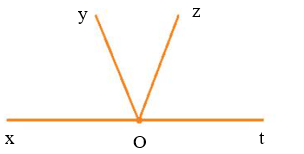
Các góc tạo thành: ∠xOy, ∠yOz, ∠zOt, ∠xOz, ∠yOt, ∠xOt .
Vậy hình a) có 6 góc.
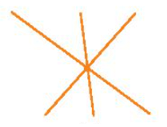
b) Đặt tên: đỉnh A và các tia Aa, Ab, Ac, Ad, Ae, Ag như hình vẽ.
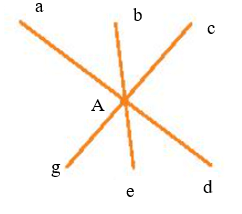
Các góc tạo thành: ∠aAb, ∠bAc, ∠cAd, ∠dAe, ∠eAg, ∠gAa, ∠aAc, ∠cAe, ∠eAa, ∠aAd, ∠bAd, ∠dAg, ∠gAb, ∠bAe, ∠cAg .
Vậy hình b) có 15 góc.
Nhận xét:
a) Số đỉnh chung của các tia là: 1;
Số các tia là: 4;
Số góc tạo thành: 4 . 3 : 2 = 6 (góc).
b) Số đỉnh chung của các tia là: 1;
Số các tia là: 6;
Số góc tạo thành: 6 . 5 : 2 = 15 (góc).
Vậy nếu đỉnh chung có n tia thì:
Tổng số các góc được tạo thành là: n . (n − 1) : 2 (góc).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
Vẽ hai đường thẳng trước, có hai khả năng xảy ra:
* Khả năng 1: Hai đường thẳng đó song song với nhau.
Ta tiếp tục vẽ thêm một đường thẳng thứ ba song song hoặc cắt cả hai đường thẳng kia.
- Trường hợp 1: Đường thẳng thứ ba song song cả hai đường thẳng kia thì ba đường thẳng này không có giao điểm nào.
Vì ba đường thẳng này không có giao điểm nào nên không có góc nào tạo ra trong trường hợp này.
- Trường hợp 2: Đường thẳng thứ ba cắt cả hai đường thẳng kia thì ta có hai giao điểm A và B.
Từ hai điểm gốc A, B, đặt các tia Aa, Ab, Ac, Bd, Be, Bg (như hình vẽ).
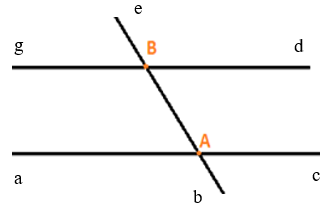
Các góc tạo thành: ∠aAb, ∠bAc, ∠aAe, ∠eAc, ∠aAc, ∠dBe, ∠eBg, ∠dBb, ∠bBg, ∠dBg, ∠bAe, ∠bBe.
Vậy hình trên có 12 góc.
* Khả năng 2: Hai đường thẳng đó cắt nhau cắt nhau tại điểm A.
Ta tiếp tục vẽ thêm một đường thẳng thứ ba cắt cả hai đường thẳng kia.
- Trường hợp 1: Đường thẳng thứ ba cắt cả hai đường thẳng kia và đi qua giao điểm A thì ta có một giao điểm A.
Từ điểm gốc A, đặt các tia Aa, Ab, Ac, Ad, Ae, Ag (như hình vẽ).
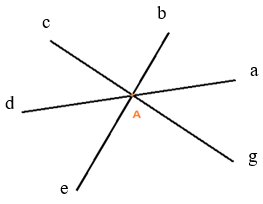
Các góc tạo thành: ∠aAb, ∠bAc, ∠cAd, ∠dAe, ∠eAg, ∠gAa, ∠aAc, ∠cAe, ∠eAa, ∠aAd, ∠bAd, ∠dAg, ∠gAb, ∠bAe, ∠cAg .
Vậy hình trên có 15 góc.
- Trường hợp 2: Đường thẳng thứ ba cắt cả hai đường thẳng kia và không đi qua giao điểm A thì ta có ba giao điểm A, B và C (như hình vẽ).
Từ ba điểm gốc A, B, C đặt các tia Ah, Ak, Bp, Bq, Cm, Cn (như hình vẽ).
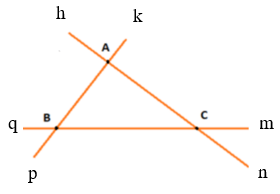
Các góc tạo thành: ∠hAk, ∠kAn, ∠hAp, ∠pAn, ∠hAn, ∠pAk, ∠pBq, ∠pBm, ∠qBk, ∠kBm, ∠mBq, ∠pBk, ∠mCn, ∠mCh, ∠nCq, ∠qCh, ∠nCh, ∠mCq .
Vậy hình trên có 18 góc.
*Nhận xét:
- Hình thứ nhất: Ba đường thẳng không có điểm chung nên không có góc nào tạo ra.
- Hình thứ hai: 2 đỉnh chung, mỗi đỉnh có 4 tia.
Vậy số góc tạo thành là 2 . 4 . 3 : 2 = 12 góc.
- Hình thứ ba: 1 đỉnh chung, có 6 tia.
Vậy số góc tạo thành là 6 . 5 : 2 = 15 (góc).
- Hình thứ tư: 3 đỉnh chung, mỗi đỉnh có 4 tia.
Vậy số góc tạo thành là 3 . 4 . 3 : 2 = 18 (góc).
Vậy nếu đỉnh chung có n tia thì:
Tổng số các góc được tạo thành là: n . (n − 1) : 2 (góc).
Lời giải
Lời giải:
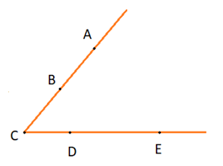
Dễ thấy:
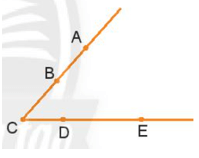
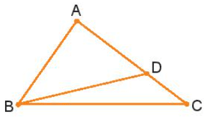
a) Góc ABC là góc bẹt (đỉnh A, hai tia là BA, BC). Góc ABC có trong hình.
b) Góc ACD có đỉnh C, hai tia là CA và CD. Góc ACD có trong hình.
c) Góc ADC không có trong hình do không nối tia DA.
d) Góc BCD có đỉnh C, hai tia là CB và CD. Góc BCD có trong hình.
e) Góc EBD không có trong hình do không nối tia BE, BD.
g) Góc AEB không có trong hình do không nối tia EA, EB.
Do đó các góc có trong hình là: góc ABC, góc ACD, góc BCD.
Vậy các phương án phù hợp là: a), b), d).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
-
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
-
Dạng 1: Thực hiện tính, viết dưới dạng lũy thừa
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 2)
-
Dạng 4: Trung điểm của đoạn thẳng có đáp án
-
Dạng 1: tỉ số của hai đại lượng có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận