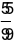Tìm ƯCLN của 25, 45 và 225 bằng cách phân tích các số ra thừa số nguyên tố.
A.18
B.3
C.15
D.5
Quảng cáo
Trả lời:
Ta phân tích các số đã cho ra thừa số nguyên tố, ta được:
25 = 5 . 5 = 52
45 = 3 . 15 = 3 . 3 . 5 = 32. 5
225 = 9 . 25 = 32. 52
Các thừa số nguyên tố chung là 5, với số mũ nhỏ nhất là 1.
Vậy ƯCLN(25, 45, 225) = 51= 5.
Chọn đáp án D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta thấy các phân số đã cho ở phần đáp án đều chưa phải là phân số tối giản, do đó ta đi rút gọn các phân số đó.
Để rút gọn các phân số đưa về tối giản, ta chia cả tử và mẫu của phân số đó cho ƯCLN của tử và mẫu.
+) 
Ta có: 20 chia hết cho 10 nên ƯCLN(10, 20) = 10
Nên 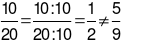 . Do đó đáp án A sai.
. Do đó đáp án A sai.
+) 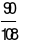
Ta có: ƯCLN(90, 108) = 18
Nên 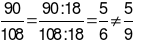 . Do đó đáp án B sai.
. Do đó đáp án B sai.
+) 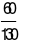
Ta có: ƯCLN(60, 130) = 10
Khi đó: 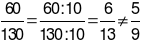 . Do đó đáp án C sai.
. Do đó đáp án C sai.
+) 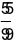
Ta có: ƯCLN(55, 99) = 11
Khi đó: 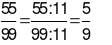 . Do đó đáp án D đúng.
. Do đó đáp án D đúng.
Chọn đáp án D.
Câu 2
A.{1; 2; 3}
B.{1; 2; 3; 6}
C.{1; 2; 3; 4}
D.{1; 2; 3; 4; 6}
Lời giải
Ta đi tìm các ước của 12, 18 và 24:
Các ước của 12 là: 1; 2; 3; 4; 6; 12
Các ước của 18 là: 1; 2; 3; 4; 6; 9; 18
Các ước của 24 là: 1; 2; 3; 4; 6; 8; 12; 24
Suy ra, ƯC(12, 18, 24) = {1; 2; 3; 6}.
Chọn đáp án B.
Câu 3
A.ƯCLN(a, b) = 3 . 7
B.ƯCLN(a, b) = 32. 72
C.ƯCLN(a, b) = 24. 5
D.ƯCLN(a, b) = 24. 32. 5 . 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
 bằng phân số nào sau đây?
bằng phân số nào sau đây?