Câu hỏi:
12/07/2024 2,692Cho hình bình hành ABCD. Gọi M là trung điểm của AB. Từ A kẻ đường thẳng song song với MC cắt DC tại N.
a) Chứng minh: Tứ giác AMCN là hình bình hành.
b) Trên thì BC lấy điểm I sao cho: CI = BC Chứng mình: AC = DI.
c) Gọi O là giao điểm của AC và MN. Chứng minh: NO là đường trung bình của ΔACD.
d) Chứng minh: MC // NI.
Câu hỏi trong đề: Đề thi Giữa kì 1 Toán 8 có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
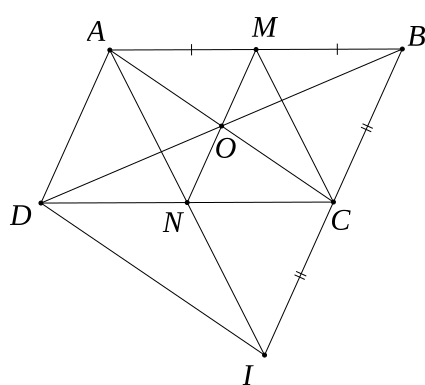
a) Ta có ABCD là hình bình hành (gt)
⇒ AB // CD; AB = CD; AD // BC; AD = BC
Mà M thuộc AB, N thuộc DC ⇒ AM // NC
Xét tứ giác AMCN có:
AM // NC (chứng minh trên)
AN // MC (giả thiết)
⇒ Tứ giác AMCN là hình bình hành.
b) AD // BC; I thuộc BC
⇒ AD // CI
Vì AD = BC (cmt); CI = BC (gt)
⇒ AD = CI
Xét tứ giác ACID có:
AD // CI (cmt)
AD = CI (cmt)
⇒ tứ giác ACID là hình bình hành
⇒ AC = DI.
c) AMCN là hình bình hành
⇒ AM = NC; O là trung điểm của AC
mà \[AM = \frac{1}{2}AB\] (M là trung điểm AB); AB = CD (cmt)
\[ \Rightarrow NC = \frac{1}{2}CD\]
⇒ N là trung điểm của CD
Xét ΔACD có:
O là trung điểm của AC (cmt)
N là trung điểm của CD (cmt)
⇒ NO là đường trung bình của ΔACD.
d) Tứ giác ACID có:
AC = DI
AD // CI
⇒ ACID là hình bình hành
Có N là trung điểm của CD
⇒ N là trung điểm AI
⇒ AN = NI, I thuộc AN
Ta có: MC // AN (AMCN là hình bình hành); I thuộc AN
⇒ MC // NI.
Nhà sách vietjack
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 4:
Tứ giác ABCD có \(\widehat A = 120^\circ \), \(\widehat B = 80^\circ \), \(\widehat C = 100^\circ \) thì số đo góc \(\widehat D\) là:
Xem đáp án »
23/03/2022
798
Câu 5:
Với giá trị của x = 15 thì giá trị của biểu thức x2– 10x + 26 là:
Xem đáp án »
23/03/2022
670
Câu 6:
a) Rút gọn biểu thức A = (x – 3)(x2+ 3x + 9) + x2(2 – x).
b) Cho biểu thức: B = x2– 4 – (x + 2)(x – 1). Tính giá trị biểu thức B với x = –1.
Xem đáp án »
23/03/2022
592
🔥 Đề thi HOT:
-
Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án (Đề 1)
-
Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
10 Bài tập Nhận biết hai hình đồng dạng, hai hình đồng dạng phối cảnh (có lời giải)
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận