Trong tất cả các hình nón nội tiếp trong hình cầu có thể tích bằng bán kính r của hình nón có diện tích xung quanh lớn nhất là
Trong tất cả các hình nón nội tiếp trong hình cầu có thể tích bằng bán kính r của hình nón có diện tích xung quanh lớn nhất là
A.
B.
C.
D. r = 3
Quảng cáo
Trả lời:
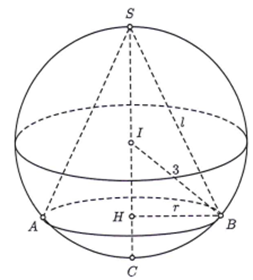
Vì hình cầu có thể tích bằng nên bán kính hình cầu là R = 3.
Diện tích xung quanh của hình nón
Gọi chiều cao của hình nón là h khi đó
Ta có suy ra
Lại có nên
Ta có
Hay dấu đẳng thức xảy ra khi h = 4.
Khi đó
Suy ra lớn nhất bằng khi
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
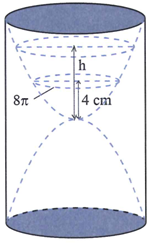
Gọi l là chiều cao của khối trụ cần tìm ta có
Cắt chiếc đồng hồ cát theo một mặt phẳng chứa trục dọc
của nó và gắn hệ trục Oxy với gốc tọa độ O là điểm giao
giữa hai Parabol, mỗi đơn vị trên trục dài 1cm.
Khi đó gọi B là điểm đo chiều cao của lượng cát lúc ban đầu,
A là điểm đo chiều cao của lượng cát lúc còn 4 cm và C
là điểm nằm ngang với A trên thành Parabol phía trên
như hình vẽ. Theo giả thiết
suy ra (P) có phương trình
Thể tích ban đầu của cát là 12,72.10 = 127,2cm3
Thể tích này bằng thể tích của khối tròn xoay khi
quay hình phẳng giới hạn bởi đường
và các đường y = 0; y = h xoay quanh trục Oy
Vậy ta có
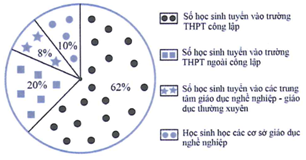
Câu 2
Lời giải
Đáp án A
Ta có
Thay
=>
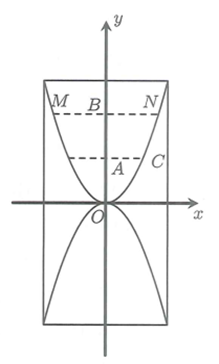
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 5 < S < 8
B. 8 < S < 12
C. 12 < S < 16
D. 16 < S < 20
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.