Câu hỏi:

05/05/2022 1,745

Một bộ pha trà bằng thủy tinh có bình tổng và các tách đều là dạng hình trụ. Bình tổng có chiều cao gấp đôi đường kính đáy, tách trà có bán kính đáy bằng một nửa bán kính đáy bình tổng và có chiều cao bằng một phần ba chiều cao bình tổng. Có ba người ngồi thưởng trà, mỗi lượt người thưởng trà chỉ uống vừa đúng ba phần tư lượng nước có trong chén trà rồi lại châm thêm nước trà từ bình tổng vào chén. Hỏi sau mấy lần rót nước trà vào các chén thì hết nước trà trong bình tổng, biết rằng thể tích nước trà ban đầu có trong bình tổng chiếm ba phần tư thể tích của bình và mỗi lần rót trà thì chỉ rót vừa đủ ba phần tư thể tích của chén trà.

A. 4

B. 5

C. 6

D. 7

Xem lời giải

Câu hỏi trong đề: Bộ 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2023 - 2024 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án B

Gọi bán kính đáy bình tổng pha trà là R, khi đó chiều cao của bình là 4R, bán kính đáy chén trà là $\frac{R}{2}$ và chiều cao chén trà là $\frac{1}{3} .4 R = \frac{4}{3} R$ .

Thể tích nước trà có trong bình tổng là: $V = \frac{3}{4} . π . R^{2} .4 R = 3 π R^{3}$ .

Thể tích nước trà trong mỗi chén ở lượt rót đầu tiên, chiếm ba phần tư thể tích của chén và bằng: $V_{c} = \frac{3}{4} π {(\frac{R}{2})}^{2} \frac{4}{3} R = \frac{1}{4} π R^{3} = \frac{1}{12} V$ .

Sau khi rót 3 chén cho 3 người thưởng trà, lượng nước trong bình tổng sẽ còn lại là: $V - 3. \frac{1}{12} V = \frac{3}{4} V$ .

Sau lượt thưởng trà lần thứ nhất, nước trong chén trà còn lại $\frac{1}{4} V_{c}$ , cần châm thêm vào 3 chén trà mỗi chén $\frac{3}{4} V_{c}$ để lượng nước trà trong mỗi chén đủ $\frac{3}{4}$ thể tích của chén như ban đầu. Tổng lượng nước trà cần thêm vào 3 chén là: $3. \frac{3}{4} V_{c} = \frac{9}{4} V_{c} = \frac{3}{16} V$ .

Như vậy, từ lần châm thêm nước thứ hai trở đi thì mỗi lần chỉ rót lượng nước là $\frac{3}{16} V$ .

Gọi số lần rót nước là n thì ta có điều kiện:

\frac{3}{4} V - (n - 1) \frac{3}{16} V \geq 0 \Leftrightarrow \frac{3}{4} - (n - 1) \frac{3}{16} \geq 0 \Leftrightarrow 4 - (n - 1) \geq 0 \Leftrightarrow n \leq 5

Như vậy vừa đủ 5 lần rót trà thì hết bình nước trà.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD biết A(1; 0; 1), B(1; 0 -3) và điểm D có hoành độ âm. Mặt phẳng (ABCD) đi qua gốc tọa độ O. Khi đó đường thẳng d là trục đường tròn ngoại tiếp hình vuông ABCD có phương trình

A. $d : \{\begin{cases} x = - 1 \\ y = t \\ z = - 1 \end{cases}$

B. $d : \{\begin{cases} x = 1 \\ y = t \\ z = - 1 \end{cases}$

C. $d : \{\begin{cases} x = - 1 \\ y = t \\ z = 1 \end{cases}$

D. $d : \{\begin{cases} x = t \\ y = 1 \\ z = t \end{cases}$

Lời giải

Đáp án A

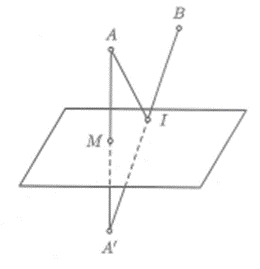
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD biết A(1; 0; 1), B(1; 0 -3), (ảnh 1)

Ta có $\vec{A B} = (0; 0; - 4) = - 4 (0; 0; 1)$ . Hay AB có vectơ chỉ phương $\vec{k} = (0; 0; 1)$ .

Mặt phẳng (ABCD) có một vectơ pháp tuyến $[\vec{O A}; \vec{O B}] = (0; 4; 0) = 4 (0; 1; 0)$ , hay $\vec{j} = (0; 1; 0)$ là một vectơ pháp tuyến của mặt phẳng (ABCD).

Vì $\{\begin{cases} A D ⊥ A B \\ A D \subset (A B C D) \end{cases}$ nên $\{\begin{cases} \vec{A D} ⊥ \vec{k} \\ \vec{A D} ⊥ \vec{j} \end{cases}$ .

Đường thẳng AD có vectơ chỉ phương là $[\vec{j}; \vec{k}] = (1; 0; 0)$ .

Phương trình đường thẳng AD là: $\{\begin{cases} x = 1 + t \\ y = 0 \\ z = 1 \end{cases}$ . Do đó $D (1 + t; 0; 1)$ .

Mặt khác $A D = A B \Leftrightarrow \sqrt{t^{2} + 0^{2} + {(1 - 1)}^{2}} = 4 \Leftrightarrow [\begin{array}{l} t = 4 \\ t = - 4 \end{array}$ .

Vì điểm D có hoành độ âm nên D(-3; 0; 1).

Vì tâm I của hình vuông ABCD là trung điểm BD nên I = (-1; 0; -1).

Đường thẳng d là trục đường tròn ngoại tiếp hình vuông ABCD có vectơ pháp tuyến là $\vec{j} = (0; 1; 0)$ , nên phương trình đường thẳng d là: $d : \{\begin{cases} x = - 1 \\ y = t \\ z = - 1 \end{cases}$ .

Câu 2

Cho hàm số $y = \{\begin{cases} x^{2} + a x + b khi x \geq 2 \\ x^{3} - x^{2} - 8 x + 10 khi x < 2 \end{cases}$ , biết hàm số có đạo hàm tại điểm x = 2. Giá trị của ab bằng

A. 2

B. 4

C. 1

D. -8

Lời giải

Đáp án D

Để hàm số có đạo hàm tại x = 2 thì hàm số phải liên tục tại x = 2.

Do đó $\lim_{x \to 2^{-}} (x^{3} - x^{2} - 8 x + 10) = \lim_{x \to 2^{+}} (x^{2} + a x + b) \Leftrightarrow - 2 = 4 + 2 a + b \Leftrightarrow 2 a + b = - 6$ .

Hàm số có đạo hàm tại điểm x = 2 nên

$\lim_{x \to 2^{-}} \frac{f (x) - f (2)}{x - 2} = \lim_{x \to 2^{+}} \frac{f (x) - f (2)}{x - 2} \Leftrightarrow \lim_{x \to 2^{-}} \frac{x^{3} - x^{2} - 8 x + 10 - (- 2)}{x - 2} = \lim_{x \to 2 +} \frac{x^{2} + a x + b - (4 + 2 a + b)}{x - 2} \Leftrightarrow \lim_{x \to 2^{-}} (x^{2} + x - 6) = \lim_{x \to 2^{+}} (x + 2 + a) \Leftrightarrow 4 + a = 0 \Leftrightarrow a = - 4$

Suy ra b = 2. Vậy ab = -8.

Câu 3

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 1, AD = AA' = 2. Bán kính mặt cầu ngoại tiếp hình tứ diện AB'CD' bằng

A. $\sqrt{5}$

B. 3

C. $\frac{3}{2}$

D. $\frac{\sqrt{5}}{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Có bao nhiêu giá trị nguyên dương của m để bất phương trình $m {.16}^{x} - (2 m + 1) {.12}^{x} + m {.9}^{x} \leq 0$ nghiệm đúng với mọi $x \in (0; 1)$ ?

A. 6

B. 11

C. 12

D. 13

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Bạn An muốn mua tặng mẹ một món quà trị giá 1 025 000đ. Để tạo sự bất ngờ cho mẹ, bạn bí mật thực hiện kế hoạch nuôi heo đất từ số tiền tiêu vặt hàng ngày của mình như sau: Ngày đầu tiên bạn bỏ vào heo đất 5000đ, các ngày tiếp theo, mỗi ngày bạn bỏ vào heo đất nhiều hơn ngày trước đó 1000đ. Hỏi bạn An phải thực hiện kế hoạch trong bao nhiêu ngày thì có đủ tiền mua quà tặng mẹ?

A. 39 ngày.

B. 40 ngày.

C. 41 ngày.

D. 50 ngày.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Hình phẳng (H) được giới hạn bởi đồ thị (C) của hàm đa thức bậc ba và parabol (P) có trục đối xứng vuông góc với trục hoành. Phần tô đậm của hình vẽ có diện tích bằng

A. $\frac{37}{12}$

B. $\frac{7}{12}$

C. $\frac{11}{12}$

D. $\frac{5}{12}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD biết A(1; 0; 1), B(1; 0 -3) và điểm D có hoành độ âm. Mặt phẳng (ABCD) đi qua gốc tọa độ O. Khi đó đường thẳng d là trục đường tròn ngoại tiếp hình vuông ABCD có phương trình

Cho hàm sốy=x2+ax+b khi x≥2x3−x2−8x+10 khi x<2, biết hàm số có đạo hàm tại điểm x = 2. Giá trị của ab bằng

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 1, AD = AA' = 2. Bán kính mặt cầu ngoại tiếp hình tứ diện AB'CD' bằng

Có bao nhiêu giá trị nguyên dương của m để bất phương trình m.16x−2m+1.12x+m.9x≤0 nghiệm đúng với mọi x∈0;1 ?

Hình phẳng (H) được giới hạn bởi đồ thị (C) của hàm đa thức bậc ba và parabol (P) có trục đối xứng vuông góc với trục hoành. Phần tô đậm của hình vẽ có diện tích bằng

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hàm số $y = \{\begin{cases} x^{2} + a x + b khi x \geq 2 \\ x^{3} - x^{2} - 8 x + 10 khi x < 2 \end{cases}$ , biết hàm số có đạo hàm tại điểm x = 2. Giá trị của ab bằng

Có bao nhiêu giá trị nguyên dương của m để bất phương trình $m {.16}^{x} - (2 m + 1) {.12}^{x} + m {.9}^{x} \leq 0$ nghiệm đúng với mọi $x \in (0; 1)$ ?