Vật sáng AB đặt trên trục chính và vuông góc với trục chính của một thấu kính hội tụ có tiêu cự 20cm. Để ảnh của vật cùng chiều với vật và cách thấu kính 30cm thì vật cách thấu kính một khoảng bằng bao nhiêu?
A. 60 cm.
Quảng cáo
Trả lời:
Phương pháp:
Sử dụng công thức thấu kính: \(\frac{1}{d} + \frac{1}{{{d^\prime }}} = \frac{1}{f}\)
Cách giải:
Ảnh cùng chiều với vật ⇒ ảnh đó là ảnh ảo
Tiêu cự của thấu kính hội tụ \(f = 20\;{\rm{cm}}\)
Áp dụng công thức thấu kính ta có: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{{d^\prime }}} \Leftrightarrow \frac{1}{{20}} = \frac{1}{d} + \frac{1}{{ - 30}} \Rightarrow d = 12\;{\rm{cm}}\)
Chọn D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Phương pháp:
Công thức liên hệ giữa tần số và bước sóng: \(f = \frac{c}{\lambda } \Rightarrow f - \frac{1}{\lambda }\)
Bước sóng theo thứ tự tăng dần: Tia tử ngoại, ánh sáng nhìn thấy, tia hồng ngoại
Cách giải:
Bảng thang sóng điện từ:
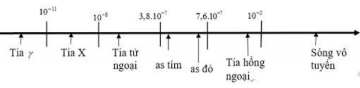
Có \(f = \frac{c}{\lambda } \Rightarrow f - \frac{1}{\lambda }\)
Tần số các sóng điện từ theo thứ tự giảm dần là: Tia tử ngoại, ánh sáng nhìn thấy, tia hồng ngoại.
Chọn A.
Câu 2
Lời giải
Phương pháp:
+ Bước sóng:
+ Điều kiện có cực đại giao thoa: \({d_2} - {d_1} = k\lambda ;k \in Z\)
Cách giải:
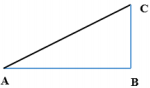
Phương trình dao động của hai nguồn:
\({u_A} = {u_B} = 5\cos \left( {20\pi t + \frac{{3\pi }}{4}} \right)({\rm{cm}};s)\)
Tốc độ truyền sóng: \(v = 0,2\;{\rm{m}}/{\rm{s}}\)
Bước sóng:
Bài cho \(AB = 30\;{\rm{cm}} \Rightarrow {\rm{AB}} = 15\lambda \)
Áp dụng định lí Pitago trong tam giác vuông ABC ta có: \(A{C^2} = A{B^2} + B{C^2} \Rightarrow A{B^2} = A{C^2} - B{C^2}\)
Mà:
Mặt khác: \({d_2} - {d_1} = k\lambda \left( 2 \right)\) (cực đại)
Từ (1) và (2) \( \Rightarrow {d_2} + {d_1} = \frac{{225}}{k}\lambda \)
Để cực đại cùng pha thì k và \(\frac{{225}}{k}\) hoặc cùng chẵn hoặc cùng lẻ, ở đây chỉ có k lẻ thỏa mãn.
Lại có: \({d_2} + {d_1} > 15\lambda \) (tổng hai cạnh bất kì của một tam giác luôn lớn hơn cạnh còn lại)
Lập bảng tìm các giá trị của k thỏa mãn:
|
k |
1 |
3 |
5 |
9 |
|
225 |
75 |
45 |
25 |
Để gần B nhất thì \({\left( {{d_2} + {d_1}} \right)_{\min }} \Leftrightarrow {\left( {\frac{{225}}{k}\lambda } \right)_{\min }} \Leftrightarrow {k_{\max }} = 9\)
Chọn D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.