Câu hỏi:
18/05/2022 664
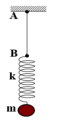
Một con lắc lò xo gồm lò xo nhẹ có độ cứng k = 50 N/m, vật nhỏ có khối lượng m = 250 g. Đầu lò xo gắn vào sợi dây AB mềm, nhẹ, không dãn như hình vẽ. Từ vị trí cân bằng, truyền cho vật vận tốc \(v = 100\sqrt 2 \;{\rm{cm}}/{\rm{s}}\) hướng thẳng đứng xuống dưới. Lấy \(g = 10\;{\rm{m}}/{{\rm{s}}^2}\), gốc thời gian \({t_0} = 0\) lúc truyền vận tốc cho vật. Tốc độ trung bình của vật từ \({t_0} = 0\) cho đến khi nó đạt độ cao cực đại lần thứ nhất là
Đáp án chính xác
Câu hỏi trong đề: 30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp:
Độ biến dạng của lò xo khi ở vị trí cân bằng: \(\Delta l = \frac{{mg}}{k}\)
Tần số góc của con lắc lò xo:
Tốc độ của vật ở vịt rí cân bằng: \({v_{\max }} = \omega A\)
Công thức độc lập với thời gian: \({v^2} = \omega \sqrt {{A^2} - {x^2}} \)
Thời gian chuyển động ném thẳng đứng lên: \(t = \frac{v}{g}\)
Độ cao vật đạt được trong chuyển động ném thẳng đứng hướng lên: \({h_{\max }} = \frac{{{v^2}}}{{2g}}\)
Sử dụng vòng tròn lượng giác và công thức: \(\Delta t = \frac{{\Delta \varphi }}{\omega }\)
Tốc độ trung bình: \({v_\phi } = \frac{S}{t}\)
Cách giải:
Tần số góc của con lắc là:
Độ biến dạng của lò xo khi ở vị trí cân bằng là:
\(\Delta l = \frac{{mg}}{k} = \frac{{0,25.10}}{{50}} = 0,05(\;{\rm{m}}) = 5(\;{\rm{cm}})\)
Nhận xét: con lắc dao động khi lực đàn hồi có độ lớn bằng 0, dây bị chùng, hệ chuyển động với gia tốc trọng trường g
→ Từ thời điểm vật đạt li độ -5 cm đến khi nó đạt độ cao cực đại lần thứ nhất, vật chuyển động giống như chuyển động ném thẳng đứng lên với vận tốc v
Ta có vòng tròn lượng giác:
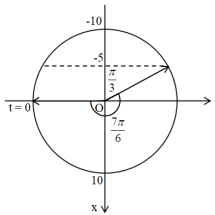
Vật dao động điều hòa trong khoảng thời gian từ thời điểm đầu đến thời điểm đầu tiên lò xo không biến dạng (x = -5 cm), vecto quay được góc là:
Quãng đường vật dao động điều hòa là:
\({s_1} = 2A + (A - \Delta l) = 3A - \Delta l = 3.10 - 5 = 25(\;{\rm{cm}})\)
Ở li độ x = -5 cm, áp dụng công thức độc lập với thời gian, ta có vận tốc của vật là:
Vật chuyển động ném lên, quãng đường vật chuyển động được đến khi dừng lại là:
\({s_2} = {h_{\max }} = \frac{{{v^2}}}{{2g}} = \frac{{{{(0,5\sqrt 6 )}^2}}}{{2.10}} = 0,075(\;{\rm{m}}) = 7,5(\;{\rm{cm}})\)
Thời gian vật chuyển động ném lên là: \({t_2} = \frac{v}{g} = \frac{{0,5\sqrt 6 }}{{10}} = \frac{{\sqrt 6 }}{{20}}(s)\)
Tốc độ trung bình của vật là:
\({v_{tb}} = \frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \frac{{25 + 7,5}}{{\frac{{7\pi }}{{60\sqrt 2 }} + \frac{{\sqrt 6 }}{{20}}}} \approx 85,16(\;{\rm{cm}}/{\rm{s}})\)
Chọn D.
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Một mạch dao động LC, với cuộn cảm thuần L = 9 mH. Trong quá trình dao động, hiệu điện thế cực đại giữa hai bản tụ là 12 V. Tại thời điểm điện tích trên bản tụ có độ lớn q = 24 nC thì dòng điện trong mạch có cường độ \(i = 4\sqrt 3 mA\). Chu kì dao động riêng của mạch bằng
Xem đáp án »
18/05/2022
1,589
Câu 3:
Trong thí nghiệm Y-âng về giao thoa với ánh sáng đơn sắc, khoảng cách giữa hai khe là 1 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn là 2 m. Trong hệ vân trên màn, vân sáng bậc 3 cách vân trung tâm 2,4 mm. Bước sóng của ánh sáng đơn sắc dùng trong thí nghiệm là
Xem đáp án »
18/05/2022
1,347
Câu 4:
Dùng một ampe kế nhiệt để đo cường độ dòng điện trong một mạch điện xoay chiều, số chỉ của ampe kế cho biết
Xem đáp án »
18/05/2022
1,202
Câu 5:
Hạt α có động năng 5 MeV bắn vào một hạt nhân \(_4^9Be\) đứng yên, gây ra phản ứng tạo thành một hạt \(^{12}C\) và một hạt nơtron. Hai hạt sinh ra có vectơ vận tốc hợp với nhau một góc 800. Cho biết phản ứng tỏa ra năng lượng 5,6 MeV. Coi khối lượng xấp xỉ bằng số khối. Động năng của hạt nhân 12C có thể bằng
Xem đáp án »
18/05/2022
861
Câu 6:
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình li độ lần lượt là \({x_1} = {A_1}\cos \left( {10t + \frac{\pi }{6}} \right)(cm);{x_2} = 4\cos (10t + \varphi )(cm)\) (t tính bằng s), \({A_1}\) có giá trị thay đổi được. Phương trình dao động tổng hợp của vật có dạng \(x = A\cos \left( {\omega t + \frac{\pi }{3}} \right)(cm)\). Độ lớn gia tốc lớn nhất của vật có thể nhận giá trị là
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình li độ lần lượt là \({x_1} = {A_1}\cos \left( {10t + \frac{\pi }{6}} \right)(cm);{x_2} = 4\cos (10t + \varphi )(cm)\) (t tính bằng s), \({A_1}\) có giá trị thay đổi được. Phương trình dao động tổng hợp của vật có dạng \(x = A\cos \left( {\omega t + \frac{\pi }{3}} \right)(cm)\). Độ lớn gia tốc lớn nhất của vật có thể nhận giá trị là
Xem đáp án »
18/05/2022
728
Câu 7:
Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu đoạn mạch AB mắc nối tiếp theo thứ tự gồm cuộn cảm thuần L, biến trở R và tụ điện C. Gọi ULR là điện áp hiệu dụng ở hai đầu đoạn mạch gồm cuộn cảm thuần L và biến trở R, UC là điện áp hiệu dụng ở hai đầu tụ C, UL là điện áp hiệu dụng hai đầu cuộn cảm thuần L. Hình bên là đồ thị biểu diễn sự phụ thuộc của, \[{U_{LR}},{U_L},{U_C}\] theo giá trị của biến trở R. Khi \[R = 1,5{R_0}\] thì hệ số công suất của đoạn mạch AB xấp xỉ là
Xem đáp án »
18/05/2022
687
🔥 Đề thi HOT:
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 2)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 6)
-
Đề thi thử tốt nghiệp THPT môn Vật lí Cụm các trường THPT , Các trung tâm GDTX , GDNN - GDTX Tỉnh Bắc Ninh có đáp án
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Chuyên Phan Bội Châu- Nghệ An - lần 1 có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận