Câu hỏi:

19/05/2022 626

Đặt điện áp $u = 180\sqrt 2 \cos \omega {\rm{t}}({\rm{V}})$ (với ω không đổi) vào hai đầu đoạn mạch AB gồm đoạn mạch AM mắc nối tiếp với đoạn mạch MB. Đoạn mạch AM chỉ có điện trở thuần R đoạn mạch MB gồm tụ điện có điện dung C mắc nối tiếp với cuộn cảm thuần có độ tự cảm L thay đổi được. Điều chỉnh giá trị L và thấy rằng: khi điện áp u và cường độ dòng điện trong mạch lệch pha nhau ${\varphi _1}$ thì điện áp hiệu dụng ở hai đầu đoạn mạch AM là U, khi điện áp u và cường độ dòng điện trong mạch lệch pha nhau ${\varphi _2}$ thì điện áp hiệu dụng ở hai đầu đoạn mạch AM là $\sqrt 3 U$. Biết ${\varphi _1} + {\varphi _2} = {90^0}$. Giá trị của U là

A. 180 V.

B. 135 V.

C. 60 V.

D. 90V.

Xem lời giải

Câu hỏi trong đề: 30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương pháp:

+ Vận dụng pha dao động trong đoạn mạch xoay chiều

+ Sử dụng giản đồ véctơ quay.

+ Sử dụng hệ thức lượng trong tam giác.

Cách giải:

Do U hai đầu đoạn mạch không đổi và ${u_R} \bot {u_{LC}}$

⇒Khi L thay đổi thì tập hợp các điểm M là đường tròn đường kính là hiệu điện thế giữa hai đầu đoạn mạch U =180 V

Mặt khác, độ lệch pha giữa u và I cũng là độ lệch pha giữa $u_{R} v à u$

Từ đó, ta có giản đồ véctơ điện áp như hình vẽ:

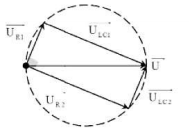
$Đặt điện áp $u = 180\sqrt 2 \cos \omega {\rm{t}}({\rm{V}})$ (với ω không đổi) vào hai đầu đoạn mạch AB gồm đoạn (ảnh 1)$

Từ giản đồ ta suy ra ${u_{{R_1}}} \bot {u_{{R_2}}} \Rightarrow U_{{R_1}}^2 + U_{{R_2}}^2 = U_{AB}^2 \Leftrightarrow {U^2} + 3{U^2} = {180^2} \Rightarrow U = 90\;{\rm{V}}$

Chọn D.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong thí nghiệm Y-âng về giao thoa ánh sáng đơn sắc, gọi i là khoảng vân, khoảng cách từ vân sáng trung tâm đến vân tối thứ hai là

A. 2i

B. 2,5i

C. i

D. 1,5i

Lời giải

Phương pháp:

Sử dụng biểu thức xác định vị trí vân tối: ${x_t} = \left( {k + \frac{1}{2}} \right)i$

Cách giải:

Vị trí vân tối: ${x_t} = \left( {k + \frac{1}{2}} \right)i$

Vân tối thứ hai ứng với k =1 ⇒Khoảng cách từ vân sáng trung tâm đến vân tối thứ hai: ${x_{t2}} = \left( {1 + \frac{1}{2}} \right)i = \frac{3}{2}i$

Chọn D.

Câu 2

Một sóng điện từ truyền qua điểm M trong không gian, cường độ điện trường và cảm ứng từ tại M biến thiên điều hòa với giá trị cực đại lần lượt là E₀và B₀. Tại một thời điểm nào đó, cường độ điện trường và cảm ứng từ tại M lần lượt là E và B. Hệ thức nào sau đây đúng?

\frac{E}{E_{0}} = - \frac{B}{B_{0}}

B. $\frac{E}{{{E_0}}} = \frac{B}{{{B_0}}}$

C. ${\left( {\frac{E}{{{E_0}}}} \right)^2} + {\left( {\frac{B}{{{B_0}}}} \right)^2} = 1$

D. ${\left( {\frac{E}{{{E_0}}}} \right)^2} + {\left( {\frac{B}{{{B_0}}}} \right)^2} = 2$

Lời giải

Phương pháp:

Trong quá trình truyền sóng, vecto cường độ điện trường $\overrightarrow E $ và vecto cảm ứng từ $\overrightarrow B $ biến thiên tuần hoàn theo không gian và thời gian, và luôn đồng pha.

Cách giải:

Do $\overrightarrow E $ và $\overrightarrow B $ biến thiên cùng pha với nhau nên: $\frac{E}{{{E_0}}} = \frac{B}{{{B_0}}}{\rm{ hay }}{\left( {\frac{E}{{{E_0}}}} \right)^2} = {\left( {\frac{B}{{{B_0}}}} \right)^2}$

Chọn B.

Câu 3

Đặt điện áp xoay chiều $u = U\sqrt 2 \cos \omega t(U > 0)$ vào hai đầu đoạn mạch RLC mắc nối tiếp. Gọi Z và I lần lượt là tổng trở và cường độ dòng điện hiệu dụng trong đoạn mạch. Hệ thức nào sau đây đúng?

A. $Z = UI$

B. $U = IZ$

C. $U = {I^2}Z$

D. $Z = {I^2}U$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong thí nghiệm Y-âng về giao thoa ánh sáng, khe S cách đều hai khe S₁ S₂, và ánh sáng phát ra là ánh sáng đơn sắc có bước sóng λ = 500nm. Trên màn, tại hai điểm M và N là các vân tối ở hai phía so với vân sáng trung tâm. Giữa M và N có 9 vân sáng. Hiệu các khoảng cách $M\;{{\rm{S}}_1} - M\;{{\rm{S}}_2} = 1,75\mu m$. Hiệu các khoảng cách $N{S_1} - N{S_2}$ có giá trị bằng

A. −2,25μm

B. −2,75μm

C. 2,25μm

D. 2,75μm

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một con lắc lò xo dao động điều hòa theo phương thẳng đứng dọc theo trục tọa độ Ox, chiều dương hướng xuống, gốc O tại vị trí cân bằng của vật nhỏ. Chọn mốc thế năng trọng trường ở vị trí cân bằng của vật nhỏ. Hình vẽ bên là các đồ thị biểu diễn sự phụ thuộc của thế năng trọng trường và thế năng đàn hồi vào li độ x của dao động. Trong đó hiệu ${x_1} - {x_2} = 3,66cm$. Biên độ dao động A của con lắc lò xo có giá trị bằng

A. 12 cm

B. 15 cm.

C. 13 cm.

D. 14 cm.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở thuần R mắc nối tiếp tụ điện có dung kháng Z_C. Hệ số công suất của đoạn mạch là

A. $\frac{R}{{\sqrt {{R^2} + Z_C^2} }}$

B. $\frac{{\sqrt {{R^2} + Z_C^2} }}{R}$

C. $\frac{{\sqrt {\left| {{R^2} - Z_c^2} \right|} }}{R}$

D. $\frac{R}{{\sqrt {\left| {{R^2} - Z_c^2} \right|} }}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong hiện tượng giao thoa sóng nước, hai nguồn dao động theo phương vuông góc S₁ và S₂ cách nhau 10 cm. với mặt nước, cùng biên độ, cùng pha, cùng tần số 50 Hz được đặt tại hai điểm S₁, bán kính S₁, S₂ Tốc độ truyền sóng trên mặt nước là 75 cm/s. Xét các điểm trên mặt nước thuộc đường tròn tâm điểm mà phần tử tại đó dao động với biên độ cực đại cách điểm S₂ một đoạn ngắn nhất bằng

A. 8 mm.

B. 9 mm.

C. 10 mm.

D. 11 mm.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Trong thí nghiệm Y-âng về giao thoa ánh sáng đơn sắc, gọi i là khoảng vân, khoảng cách từ vân sáng trung tâm đến vân tối thứ hai là

Đặt điện áp xoay chiều \(u = U\sqrt 2 \cos \omega t(U > 0)\) vào hai đầu đoạn mạch RLC mắc nối tiếp. Gọi Z và I lần lượt là tổng trở và cường độ dòng điện hiệu dụng trong đoạn mạch. Hệ thức nào sau đây đúng?

Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở thuần R mắc nối tiếp tụ điện có dung kháng Z_C. Hệ số công suất của đoạn mạch là