Gọi m là số thực dương sao cho đường thẳng \[y = m + 1\] cắt đồ thị hàm số \[y = {x^4} - 3{x^2} - 2\] tại hai điểm A, B thỏa mãn tam giác OAB vuông tại O (O là gốc tọa độ). Kết luận nào sau đây là đúng?

Phương pháp giải:

Dựa vào giả thiết bài toán, biểu diễn mối quan hệ giữa x,y kết hợp với điều kiện của x, y để tìm hệ điều kiện.

Giải chi tiết:

Gọi x là số tấn nguyên liệu loại I, y là số tấn nguyên liệu loại II cần dùng.

Vì cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II nên ta có: \[\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 10}\\{0 \le y \le 9}\end{array}} \right..\]

Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và \[0,6{\mkern 1mu} {\mkern 1mu} kg\] chất B

⇒⇒ Từ xx tấn nguyên liệu loại I ta chiết xuất được: \[20x{\mkern 1mu} {\mkern 1mu} kg\] chất A và \[0,6y{\mkern 1mu} {\mkern 1mu} kg\]chất B.

Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được \[10{\mkern 1mu} {\mkern 1mu} kg\] chất A và \[1,5{\mkern 1mu} {\mkern 1mu} kg\] chất B

⇒ Từ y là số tấn nguyên liệu loại II  ta chiết xuất được:  \[10y{\mkern 1mu} {\mkern 1mu} kg\] chất A và \[1,5y{\mkern 1mu} {\mkern 1mu} kg\] chất B.

Như vậy ta chiết xuất được \[20x + 10y{\mkern 1mu} {\mkern 1mu} \left( {kg} \right)\] chất A và \[0,6x + 1,5y{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {kg} \right)\] chất B.

Khi đó ta có hệ điều kiện là:  \[\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 10}\\{0 \le y \le 9}\\{20x + 10y \ge 140}\\{0,6x + 1,5y \ge 9}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{0 \le x \le 10}\\{0 \le y \le 9}\\{2x + y \ge 14}\\{2x + 5y \ge 30}\end{array}} \right..\]

Phương pháp giải:

Số lượng cá thể = mật độ x diện tích khu phân bố

Giải chi tiết:

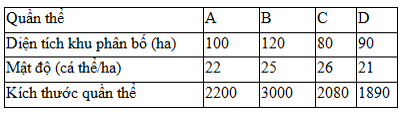
Xét các phát biểu:

I: đúng

II: đúng

III:  đúng, mật độ quần thể B sau khi tăng 5% là \[\frac{{3000 \times (1 + 0,05)}}{{120}} = 26,25\] cá thể/ ha

IV: Sai:  quần thể C tăng thêm: 2080 × 5% = 104 cá thể.