Khoảng giữa tháng 12 năm 2019, dịch viêm phổi cấp COVID-19 do chủng virus corona mới đã bùng phát tại thành phố Vũ Hán, thuộc tỉnh Hồ Bắc ở miền trung Trung Quốc. Triệu chứng của bệnh bao gồm sốt, ho, khó thở,… và có thể gây tử vong cho con người. Trong thời gian dịch bệnh diễn biến phức tạp, Bộ Y tế Việt Nam đã đưa ra các khuyến cáo phòng dịch trong đó có việc sử dụng nước rửa tay khô. Thành phần chính của nước rửa tay khô là cồn y tế (ancol etylic). Trong đó, một số loại nước rửa tay khô được bổ sung thêm chất X giúp làn da mịn màng, tươi trẻ, hạn chế nếp nhăn. Biết đốt cháy 9,89 gam X cần dùng 20,8656 lít khí O₂ (đktc) thu được CO₂ và H₂O. Hấp thụ sản phẩm cháy vào dung dịch Ba(OH)₂ dư thấy khối lượng dung dịch giảm 91,701 gam. X có công thức phân tử trùng với công thức đơn giản nhất. Công thức phân tử của X là (biết NTK: H = 1; C = 12; O = 16)

Phương pháp giải:

Dựa vào giả thiết bài toán, biểu diễn mối quan hệ giữa x,y kết hợp với điều kiện của x, y để tìm hệ điều kiện.

Giải chi tiết:

Gọi x là số tấn nguyên liệu loại I, y là số tấn nguyên liệu loại II cần dùng.

Vì cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II nên ta có: \[\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 10}\\{0 \le y \le 9}\end{array}} \right..\]

Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và \[0,6{\mkern 1mu} {\mkern 1mu} kg\] chất B

⇒⇒ Từ xx tấn nguyên liệu loại I ta chiết xuất được: \[20x{\mkern 1mu} {\mkern 1mu} kg\] chất A và \[0,6y{\mkern 1mu} {\mkern 1mu} kg\]chất B.

Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được \[10{\mkern 1mu} {\mkern 1mu} kg\] chất A và \[1,5{\mkern 1mu} {\mkern 1mu} kg\] chất B

⇒ Từ y là số tấn nguyên liệu loại II  ta chiết xuất được:  \[10y{\mkern 1mu} {\mkern 1mu} kg\] chất A và \[1,5y{\mkern 1mu} {\mkern 1mu} kg\] chất B.

Như vậy ta chiết xuất được \[20x + 10y{\mkern 1mu} {\mkern 1mu} \left( {kg} \right)\] chất A và \[0,6x + 1,5y{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {kg} \right)\] chất B.

Khi đó ta có hệ điều kiện là:  \[\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 10}\\{0 \le y \le 9}\\{20x + 10y \ge 140}\\{0,6x + 1,5y \ge 9}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{0 \le x \le 10}\\{0 \le y \le 9}\\{2x + y \ge 14}\\{2x + 5y \ge 30}\end{array}} \right..\]

Phương pháp giải:

Số lượng cá thể = mật độ x diện tích khu phân bố

Giải chi tiết:

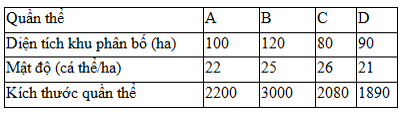
Xét các phát biểu:

I: đúng

II: đúng

III:  đúng, mật độ quần thể B sau khi tăng 5% là \[\frac{{3000 \times (1 + 0,05)}}{{120}} = 26,25\] cá thể/ ha

IV: Sai:  quần thể C tăng thêm: 2080 × 5% = 104 cá thể.