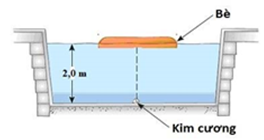
Kẻ trộm giấu viên kim cương ở dưới đáy một bể bơi. Anh ta đặt chiếc bè mỏng đồng chất hình tròn bán kính R trên mặt nước, tâm của bè nằm trên đường thẳng đứng đi qua viên kim cương. Mặt nước yên lặng và mức nước là \[h = 2,0m\]. Cho chiết suất của nước là \[n = \frac{4}{3}\]. Giá trị nhỏ nhất của R để người ở ngoài bể bơi không nhìn thấy viên kim cương gần đúng bằng:

Quảng cáo
Trả lời:
Phương pháp giải:
Điều kiện xảy ra hiện tượng phản xạ toàn phần:
Giải chi tiết:
+ Để người ở ngoài bề không quan sát thấy viên kim cương thì tia sáng từ viên kim cương đến rìa của tấm bè bị phản xạ toàn phần, không cho tia khúc xạ ra ngoài không khí.
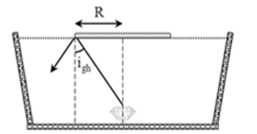
+ Góc tới giới hạn ứng với cặp môi trường nước và không khí: \[\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}} = \frac{1}{{\frac{4}{3}}} = \frac{3}{4} \Rightarrow {i_{gh}} = {48,6^0}\]
+ Từ hình vẽ, ta có :
\[\tan {i_{gh}} = \frac{{{R_{\min }}}}{h} \Rightarrow {R_{\min }} = h.\tan {i_{gh}} = 2.\tan {48,6^0} = 2,27m\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Phương pháp giải:
Dựa vào giả thiết bài toán, biểu diễn mối quan hệ giữa x,y kết hợp với điều kiện của x, y để tìm hệ điều kiện.
Giải chi tiết:
Gọi x là số tấn nguyên liệu loại I, y là số tấn nguyên liệu loại II cần dùng.
Vì cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II nên ta có: \[\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 10}\\{0 \le y \le 9}\end{array}} \right..\]
Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và \[0,6{\mkern 1mu} {\mkern 1mu} kg\] chất B
⇒⇒ Từ xx tấn nguyên liệu loại I ta chiết xuất được: \[20x{\mkern 1mu} {\mkern 1mu} kg\] chất A và \[0,6y{\mkern 1mu} {\mkern 1mu} kg\]chất B.
Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được \[10{\mkern 1mu} {\mkern 1mu} kg\] chất A và \[1,5{\mkern 1mu} {\mkern 1mu} kg\] chất B
⇒ Từ y là số tấn nguyên liệu loại II ta chiết xuất được: \[10y{\mkern 1mu} {\mkern 1mu} kg\] chất A và \[1,5y{\mkern 1mu} {\mkern 1mu} kg\] chất B.
Như vậy ta chiết xuất được \[20x + 10y{\mkern 1mu} {\mkern 1mu} \left( {kg} \right)\] chất A và \[0,6x + 1,5y{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {kg} \right)\] chất B.
Khi đó ta có hệ điều kiện là: \[\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 10}\\{0 \le y \le 9}\\{20x + 10y \ge 140}\\{0,6x + 1,5y \ge 9}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{0 \le x \le 10}\\{0 \le y \le 9}\\{2x + y \ge 14}\\{2x + 5y \ge 30}\end{array}} \right..\]
Lời giải
Phương pháp giải:
Số lượng cá thể = mật độ x diện tích khu phân bố
Giải chi tiết:
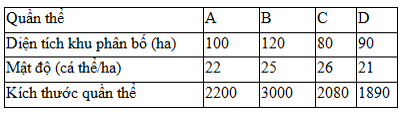
Xét các phát biểu:
I: đúng
II: đúng
III: đúng, mật độ quần thể B sau khi tăng 5% là \[\frac{{3000 \times (1 + 0,05)}}{{120}} = 26,25\] cá thể/ ha
IV: Sai: quần thể C tăng thêm: 2080 × 5% = 104 cá thể.
Câu 3
A. Nếu hôm nay trời không mưa thì tôi không ở nhà.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. take more tasks than our potential
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
