Cho mạch điện AB như hình 2. Biết các biến trở R3và R4. Bỏ qua điện trở các dây nối. Đặt vào hai đầu mạch AB hiệu điện thế không đổi U = 6V.
1. Với trường hợp ,. Mắc vào hai điểm C và D một vôn kế lí tưởng. Xác định số chỉ của vôn kế.
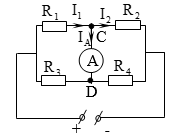
2. Với trường hợp . Mắc vào hai điểm C và D một ampe kế lí tưởng. Xác định giá trị của R4 để số chỉ của ampe kế là 0,75A và chiều dòng điện qua ampe kế từ C đến D.
3. Với trường hợp (không đổi). Thay đổi giá trị của biến trở , khi hoặc thì công suất tỏa nhiệt trên biến trở có giá trị như nhau và bằng P, khi thì công suất toả nhiệt trên biến trở đạt giá trị lớn nhất là . Cho biết và . Tìm .
Cho mạch điện AB như hình 2. Biết các biến trở R3và R4. Bỏ qua điện trở các dây nối. Đặt vào hai đầu mạch AB hiệu điện thế không đổi U = 6V.
1. Với trường hợp ,. Mắc vào hai điểm C và D một vôn kế lí tưởng. Xác định số chỉ của vôn kế.
2. Với trường hợp . Mắc vào hai điểm C và D một ampe kế lí tưởng. Xác định giá trị của R4 để số chỉ của ampe kế là 0,75A và chiều dòng điện qua ampe kế từ C đến D.
3. Với trường hợp (không đổi). Thay đổi giá trị của biến trở , khi hoặc thì công suất tỏa nhiệt trên biến trở có giá trị như nhau và bằng P, khi thì công suất toả nhiệt trên biến trở đạt giá trị lớn nhất là . Cho biết và . Tìm .
Câu hỏi trong đề: Đề thi Vật lí ôn vào 10 hệ chuyên có đáp án (Mới nhất) !!
Quảng cáo
Trả lời:
- Sơ đồ mạch: (R1ntR2)//(R3ntR4).
- Ta có : R12 = 3![]() ; R34 = 6
; R34 = 6![]() .
.
- Vì R12//R34 nên : U12 = U34 = 6V.
- Lúc đó: I1 = I12 = = 2A;
I3 = I34 = = 1A.
- Suy ra: U1 = I1.R1 = 2V; U3 = I3.R3 = 2,5V.
- Do U3 > U1 nên số chỉ của vôn kế là:
UV = U3 – U1 = 0,5 V.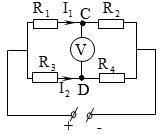
- Sơ đồ mạch: (R1//R3)nt(R2//R4).
- Ta có: R13 = ; R24 =
- Điện trở tương đương của đoạn mạch là :
Rtđ = R13 + R24
=
Cường độ dòng điện chạy qua mạch chính là:
I =
- Cường độ dòng điện chạy qua điện trở R1 và R2 lần lượt là:
- Xét tại nút C, ta có: IA = I1 – I2
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
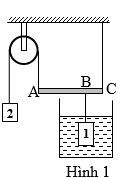
- Đoạn mạch được mắc: (R1ntR2)//(R0ntR4).
- Ta có: U04 = U.
- Công suất tiêu thụ trên điện trở R4 được tính:
P4 = .
- Đặt (1)
Có
- Theo bài ra :
- Lại có:
(Với )
- Lúc đó:
- Thay vào (1), ta được:
- Vậy
Lời giải
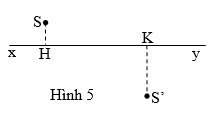
- Do S và S’ nằm khác phía trục chính xy nên thấu kính đã cho là thấu kính hội tụ. Ta có hình vẽ:
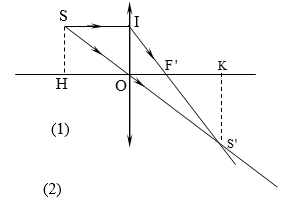
Đặt f = OF = OF’
- Theo đề:
- Do
(1)
- Do
(2)
- Với OI = SH, nên từ (1) và (2) ta được:
- Vậy tiêu cự thấu kính là 20 cm.
2.
Trường hợp cố định S, tịnh tiến thấu kính:
- Gọi: O’ là vị trí quang tâm của thấu kính sau khi dịch chuyển 1s.
+ v là tốc độ của thấu kính
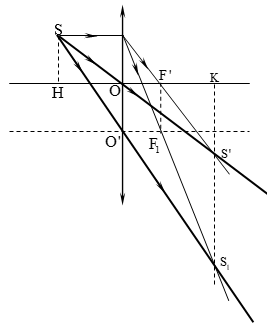
+ S1 là vị trí ảnh của S khi quang tâm thấu kính ở vị trí O’.

*Trường hợp thấu kính cố định, dịch chuyển nguồn sáng
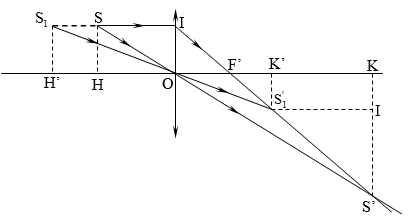


Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.