Câu hỏi:
11/07/2024 3,362Bạn Hoàng dự định mua x con cá vàng và y con cá Koi từ một trang trại cá giống. Cho biết mỗi con cá vàng có giá 35 nghìn đồng và mỗi con cá Koi có giá 150 nghìn đồng. Hoàng chỉ để dành được 1,7 triệu đồng và trại cá chỉ bán mỗi loại cá từ 10 con trở lên. Hãy viết hệ bất phương trình mô tả điều kiện ràng buộc đối với x, y.
Câu hỏi trong đề: Giải SBT Toán 10 Bài tập cuối chương 2 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì x và y lần lượt là số cá vàng và cá Koi bạn Hoàng dự định mua và trại cá chỉ bán mỗi loại cá từ 10 con trở lên nên x ≥ 10 và y ≥ 10.
Số tiền mua x con cá vàng là 35x (nghìn đồng).
Số tiền mua y con cá Koi là 150y (nghìn đồng).
Do Hoàng chỉ có 1,7 triệu đồng hay 1700 nghìn đồng nên 35x + 150y ≤ 1700 ⇔ 7x + 30y ≤ 340.
Vậy ta có hệ bất phương trình mô tả điều kiện ràng buộc đối với x, y làHot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x và y lần lượt là số bình hoa loại nhỏ và loại lớn mà bạn học sinh có thể làm được (x ≥ 0, y ≥ 0).
Đổi 90 phút = 1,5 giờ.
Ban tổ chức yêu cầu phải làm ít nhất 12 bình hoa nên x + y ≥ 12.
Số giờ để làm x bình hoa loại nhỏ là x (giờ), số giờ để làm y bình hoa loại lớn là 1,5y (giờ).
Vì học sinh này chỉ thu xếp được 15 giờ nghỉ để làm nên x + 1,5y ≤ 15.
Do đó, ta có hệ bất phương trình sau:Biểu diễn miền nghiệm của hệ bất phương trình ta được miền tam giác ABC có tọa độ các đỉnh là A(12; 0), B(15; 0), C(6; 6) (phần không gạch chéo kể cả bờ trong hình dưới).
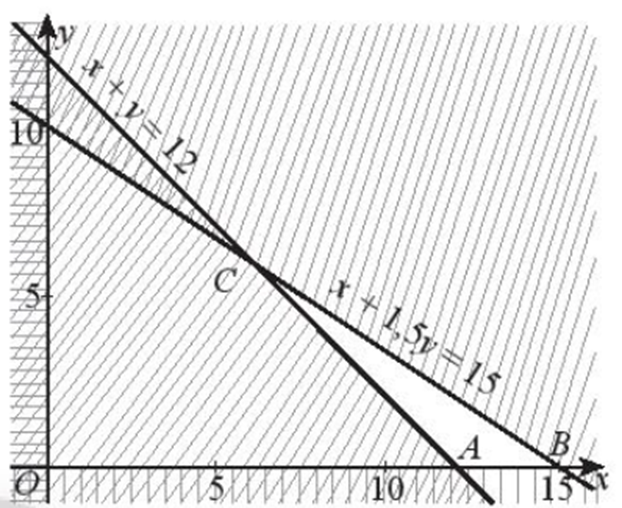
Số tiền gây quỹ là F = 100x + 200y.
Người ta chứng minh được rằng F đạt GTLN tại các đỉnh của tam giác ABC.
Ta có: F(12; 0) = 100 . 12 + 200 . 0 = 1 200
F(15; 0) = 100 . 15 + 200 . 0 = 1 500
F(6; 6) = 100 . 6 + 200 . 6 = 1 800.
Do đó, F đạt GTLN là 1 800 nghìn đồng tại đỉnh C(6; 6).
Vậy bạn đó cần làm 6 cái bình hoa mỗi loại để gây được quỹ nhiều tiền nhất.
Lời giải
Gọi x và y lần lượt là số tấn sản phẩm X và Y mà xưởng cần sản xuất (x ≥ 0, y ≥ 0) (1).
Để sản xuất x tấn sản phẩm X cần 6x tấn nguyên liệu A, 2x tấn nguyên liệu B.
Để sản xuất y tấn sản phẩm Y cần 2y tấn nguyên liệu A, 2y tấn nguyên liệu B.
Do xưởng sản xuất có 12 tấn nguyên liệu A và 8 tấn nguyên liệu B nên 6x + 2y ≤ 12 và 2x + 2y ≤ 8.
Ta có 6x + 2y ≤ 12 ⇔ 3x + y ≤ 6. (2)
2x + 2y ≤ 8 ⇔ x + y ≤ 4. (3)
Từ đó ta có hệ bất phương trình sau:Biểu diễn miền nghiệm của hệ bất phương trình ta được miền tứ giác OABC có tọa độ các đỉnh là: O(0; 0), A(0; 4), B(1; 3), C(2; 0) (miền không bị gạch trong hình sau kể cả bờ).
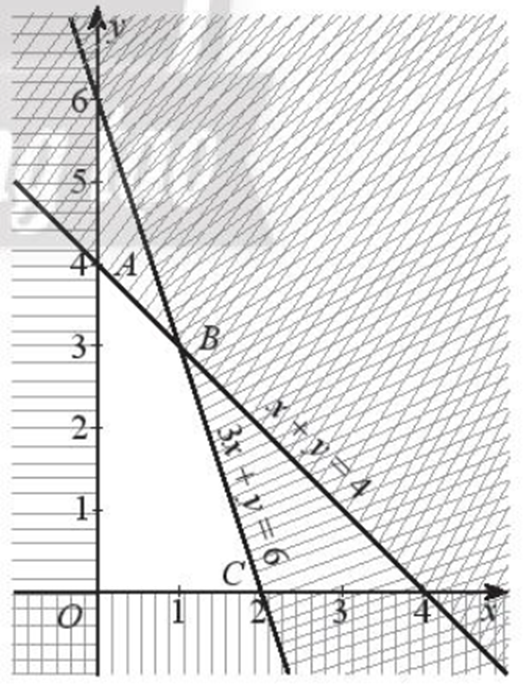
Số tiền lãi khi bán x sản phẩm X và y sản phẩm Y là F = 10x + 8y (triệu đồng).
Người ta chứng minh được rằng F đạt GTLN tại các đỉnh của tứ giác OABC.
Ta có: F(0; 0) = 10 . 0 + 8 . 0 = 0
F(0; 4) = 10 . 0 + 8 . 2 = 32
F(1; 3) = 10 . 1 + 8 . 3 = 34
F(2; 0) = 10 . 2 + 8 . 0 = 20
Do đó, F đạt GTLN là 34 triệu đồng tại đỉnh B(1; 3).
Vậy xưởng cần sản xuất 1 tấn sản phẩm X và 3 tấn sản phẩm Y thì sẽ có tổng tiền lãi cao nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
10 Bài tập Tìm hệ số, số hạng trong khai triển nhị thức Newton (có lời giải)
-
50 câu trắc nghiệm Thống kê cơ bản (phần 1)