Một xưởng sản xuất có 12 tấn nguyên liệu A và 8 tấn nguyên liệu B để sản xuất hai loại sản phẩm X, Y. Để sản xuất một tấn sản phẩm X cần dùng 6 tấn nguyên liệu A và 2 tấn nguyên liệu B, khi bán lãi được 10 triệu đồng. Để sản xuất một tấn sản phẩm Y cần dùng 2 tấn nguyên liệu A và 2 tấn nguyên liệu B, khi bán lãi được 8 triệu đồng. Hãy lập kế hoạch sản xuất cho xưởng nói trên sao cho có tổng số tiền lãi cao nhất.
Một xưởng sản xuất có 12 tấn nguyên liệu A và 8 tấn nguyên liệu B để sản xuất hai loại sản phẩm X, Y. Để sản xuất một tấn sản phẩm X cần dùng 6 tấn nguyên liệu A và 2 tấn nguyên liệu B, khi bán lãi được 10 triệu đồng. Để sản xuất một tấn sản phẩm Y cần dùng 2 tấn nguyên liệu A và 2 tấn nguyên liệu B, khi bán lãi được 8 triệu đồng. Hãy lập kế hoạch sản xuất cho xưởng nói trên sao cho có tổng số tiền lãi cao nhất.
Câu hỏi trong đề: Giải SBT Toán 10 Bài tập cuối chương 2 có đáp án !!
Quảng cáo
Trả lời:
Gọi x và y lần lượt là số tấn sản phẩm X và Y mà xưởng cần sản xuất (x ≥ 0, y ≥ 0) (1).
Để sản xuất x tấn sản phẩm X cần 6x tấn nguyên liệu A, 2x tấn nguyên liệu B.
Để sản xuất y tấn sản phẩm Y cần 2y tấn nguyên liệu A, 2y tấn nguyên liệu B.
Do xưởng sản xuất có 12 tấn nguyên liệu A và 8 tấn nguyên liệu B nên 6x + 2y ≤ 12 và 2x + 2y ≤ 8.
Ta có 6x + 2y ≤ 12 ⇔ 3x + y ≤ 6. (2)
2x + 2y ≤ 8 ⇔ x + y ≤ 4. (3)
Từ đó ta có hệ bất phương trình sau:Biểu diễn miền nghiệm của hệ bất phương trình ta được miền tứ giác OABC có tọa độ các đỉnh là: O(0; 0), A(0; 4), B(1; 3), C(2; 0) (miền không bị gạch trong hình sau kể cả bờ).
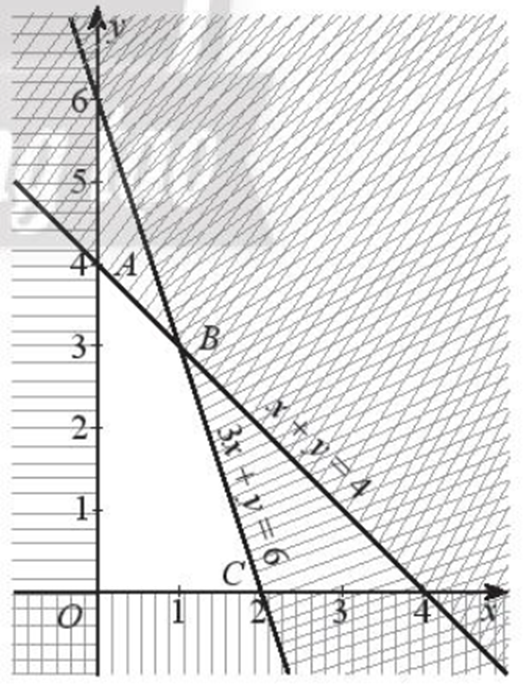
Số tiền lãi khi bán x sản phẩm X và y sản phẩm Y là F = 10x + 8y (triệu đồng).
Người ta chứng minh được rằng F đạt GTLN tại các đỉnh của tứ giác OABC.
Ta có: F(0; 0) = 10 . 0 + 8 . 0 = 0
F(0; 4) = 10 . 0 + 8 . 2 = 32
F(1; 3) = 10 . 1 + 8 . 3 = 34
F(2; 0) = 10 . 2 + 8 . 0 = 20
Do đó, F đạt GTLN là 34 triệu đồng tại đỉnh B(1; 3).
Vậy xưởng cần sản xuất 1 tấn sản phẩm X và 3 tấn sản phẩm Y thì sẽ có tổng tiền lãi cao nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x và y lần lượt là số bình hoa loại nhỏ và loại lớn mà bạn học sinh có thể làm được (x ≥ 0, y ≥ 0).
Đổi 90 phút = 1,5 giờ.
Ban tổ chức yêu cầu phải làm ít nhất 12 bình hoa nên x + y ≥ 12.
Số giờ để làm x bình hoa loại nhỏ là x (giờ), số giờ để làm y bình hoa loại lớn là 1,5y (giờ).
Vì học sinh này chỉ thu xếp được 15 giờ nghỉ để làm nên x + 1,5y ≤ 15.
Do đó, ta có hệ bất phương trình sau:Biểu diễn miền nghiệm của hệ bất phương trình ta được miền tam giác ABC có tọa độ các đỉnh là A(12; 0), B(15; 0), C(6; 6) (phần không gạch chéo kể cả bờ trong hình dưới).
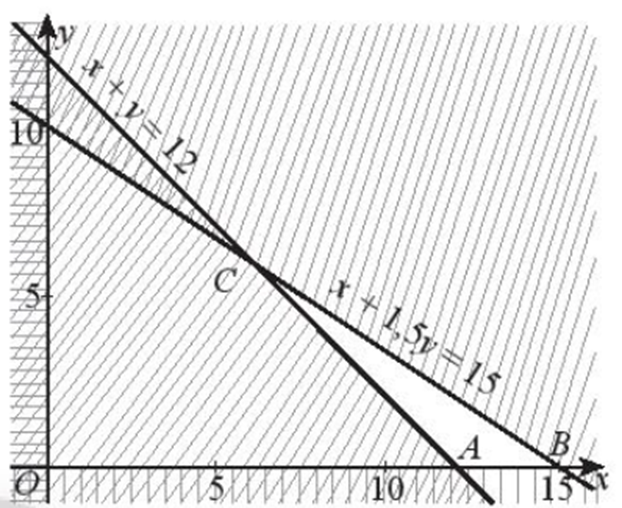
Số tiền gây quỹ là F = 100x + 200y.
Người ta chứng minh được rằng F đạt GTLN tại các đỉnh của tam giác ABC.
Ta có: F(12; 0) = 100 . 12 + 200 . 0 = 1 200
F(15; 0) = 100 . 15 + 200 . 0 = 1 500
F(6; 6) = 100 . 6 + 200 . 6 = 1 800.
Do đó, F đạt GTLN là 1 800 nghìn đồng tại đỉnh C(6; 6).
Vậy bạn đó cần làm 6 cái bình hoa mỗi loại để gây được quỹ nhiều tiền nhất.
Lời giải
Đáp án đúng là: D
Xét đáp án A, 2x – 3y – 2022 ≤ 0 ⇔ 2x – 3y ≤ 2022, đây là một bất phương trình bậc nhất hai ẩn có dạng ax + by ≤ c (a, b, c là các số thực, a, b không đồng thời bằng 0).
Xét đáp án B, 5x + y ≥ 2x + 11 ⇔ 3x + y ≥ 11, đây là một bất phương trình bậc nhất hai ẩn có dạng ax + by ≥ c (a, b, c là các số thực, a, b không đồng thời bằng 0).
Xét đáp án C, x + 2025 > 0 ⇔ x + 0y > – 2025, đây là một bất phương trình bậc nhất hai ẩn có dạng ax + by > c (a, b, c là các số thực, a, b không đồng thời bằng 0).
Xét đáp án D, , đây không phải là một bất phương trình bậc nhất hai ẩn vì nó không có một trong các dạng ax + by < c, ax + by > c, ax + by ≤ c, ax + by ≥ c với a, b, c là các số thực, a, b không đồng thời bằng 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.