Bộ 25 đề thi ôn vào 6 môn Toán chất lượng cao có đáp án - Đề 7

Ta có: $\frac{2}{7}$= 0,285714285714..

Nhận xét:

Đằng sau dấu phẩy, cụm 6 chữ số "285714" được lặp đi lặp lại.

Vì 2024 : 6 = 337 (dư 2) nên chữ số thứ 2024 sau dấu phẩy là chữ số 8.

Đáp số: 8

Ta làm bài này theo phương pháp tính ngược từ cuối lên, lần lượt theo các bước (1), (2), (3), (4), (5), (6) như bảng sau:

Vậy ban đầu Dương có 40 cái kẹo, Hà có 50 cái kẹo

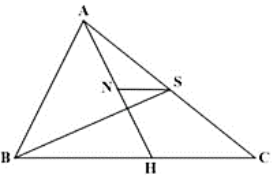
Nối điểm N với C, H với S.

Vì N là trung điểm của AH nên NH =NA=$\frac{1}{2}$AH

Ta có: S_CNH = S_CSH (vì chung đáy CH, chiều cao hạ từ N và S tới HC bằng nhau)

Mà S_CNH = $\frac{1}{2}$S_CAH (vì chung chiều cao hạ từ C tới AH, đáy NH =$\frac{1}{2}$AH)

→ S_CSH = $\frac{1}{2}$S_CAH

Mà hai tam giác này có chung chiều cao hạ từ H tới AC nên đáy SC = $\frac{1}{2}$AC

→ S_BSC = $\frac{1}{2}$ S_BAC (vì chung chiều cao hạ từ B tới AC và đây SC = AC)

→ S_ABS = $\frac{1}{2}$S_BAC = 100 : 2 = 50 (cm²)

Đáp số: 50 cm²

a) Có 12 viên bi. Do đó, Thuật sẽ có chiến thuật để luôn là người chiến thắng bằng cách như sau: Lượt đầu tiên. Chiến bốc. Tiếp đó Thuật sẽ bốc sao cho tổng số bi của Thuật và số bi của Chiến ở lượt bốc trước đó bằng 6.

Sau đó còn lại 6 viên. Bây giờ Chiến bốc 2, 3 hay 4 viên thì vẫn còn lại tương ứng là 4, 3 hay 2 viên. Và Thuật sẽ bốc số bi còn lại đó, do đó Thuật là người chiến thắng

b) Muốn Chiến là người chiến thắng thì số bi ban đầu phải chia cho 6 dư 2, 3 hoặc 4.

Thật vậy:

Giả sử số bị chia cho 6 dư 2. Khi đó:

Lần đầu tiên, Chiến bốc 2 viên. Do đó, số bi còn lại là số chia hết cho 6.

Tiếp đó đến lượt Thuật bốc. Sau khi Thuật bốc, Chiến sẽ bốc một số bị sao cho tổng số bị của Thuật và Chiến vừa bốc bằng 6.

Cứ tiếp tục như vậy Chiến sẽ là người bốc cuối cùng và Chiến luôn thắng.

Tương tự với trường hợp số bị chia cho 6 dư 3, 4. Khi đó, lần đầu tiên Chiến sẽ bốc tương ứng 3, 4 viên sau đó với cách bốc như trường hợp dư 2 đã nêu ở trên, Chiến cũng sẽ luôn thắng.