b) Chứng minh AH2 = HB.HC.

b) Lần lượt xét hai tam giác vuông ABC và ABH có +) ABC^+ACB^=180°−BAC^=90°(1) +) ABH^+BAH^=180°−AHB^=90° (2) Từ (1) và (2) nên suy ra ACB^=BAH^ (Vì cùng phụ với góc ABC^ ) Xét hai tam giác DABH và DCAH có BAH^=ACH^ cmt AHB^=CHA^ =90°⇒ΔABH∽ΔCAHg.g ⇒AHCH=BHAH⇔AH2=HB.HC (đpcm).

Câu hỏi:

19/08/2025 1,269

b) Chứng minh AH² = HB.HC.

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất) !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

b) Lần lượt xét hai tam giác vuông ABC và ABH có

+) $\hat{A B C} + \hat{A C B} = 180 ° - \hat{B A C} = 90 °$ (1)

+) $\hat{A B H} + \hat{B A H} = 180 ° - \hat{A H B} = 90 °$ (2)

Từ (1) và (2) nên suy ra $\hat{A C B} = \hat{B A H}$ (Vì cùng phụ với góc $\hat{A B C}$ )

Xét hai tam giác DABH và DCAH có

$\begin{matrix} \hat{B A H} = \hat{A C H} (c m t) \\ \hat{A H B} = \hat{C H A} (= 90 °) \end{matrix}\} \Rightarrow Δ A B H ∽ Δ C A H (g . g)$

$\Rightarrow \frac{A H}{C H} = \frac{B H}{A H} \Leftrightarrow A H^{2} = H B . H C$ (đpcm).

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một chiếc thang dài 5m dựa vào một bức tường có khoảng cách từ chân thang đến tường là 3m. Một thanh chống thẳng đứng cao 0,2m dùng để đỡ chiếc thang (như hình vẽ bên). Hỏi chiều cao a của tường từ mặt đất lên chỗ thang dựa và khoảng cách b từ chân thang đến thanh chống thẳng đứng là bao nhiêu?

Xem đáp án

Lời giải

Hướng dẫn giải

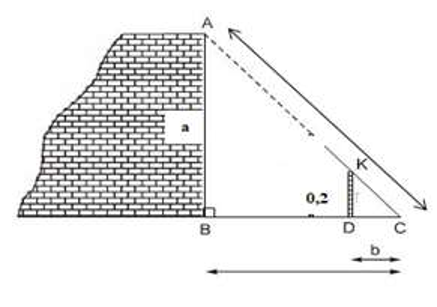
Áp dụng định lý Py-ta-go vào tam giác KDC vuông tại D có:

$K C = \sqrt{K D^{2} + D C^{2}} = \sqrt{{0,2}^{2} + b^{2}} = \sqrt{b^{2} + 0,04}$

Áp dụng định lý Ta-lét vào tam giác CBA có KD // AB nên:

$\frac{K D}{A B} = \frac{C D}{B C} = \frac{K C}{A C}$

$\Leftrightarrow \frac{0,2}{a} = \frac{b}{3} = \frac{\sqrt{b^{2} + 0,04}}{5}$

+) Với $\frac{b}{3} = \frac{\sqrt{b^{2} + 0,04}}{5}$

$\Leftrightarrow 5 b = 3 \sqrt{b^{2} + 0,04}$

Bình phương hai vế của phương trình trên nên suy ra

25b² = 9(b² + 0,04)

Û 25b² = 9b² + 0,36

Û 16b² = 0,36 Û b² = 0,0225

Þ b = 0,15 (vì b > 0)

+) Với $\frac{0,2}{a} = \frac{b}{3}$

$\Leftrightarrow a = \frac{3.0,2}{b} = \frac{0,6}{0,15} = 4$

Vậy suy ra chiều cao của tường từ mặt đất lên chỗ thang dựa là a = 4 m và khoảng cách từ chân thang đến thanh chống thẳng đứng là b = 0,15 m.

Câu 2

Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH.
a) Chứng minh DABH đồng dạng DABC.

Xem đáp án

Lời giải

Hướng dẫn giải

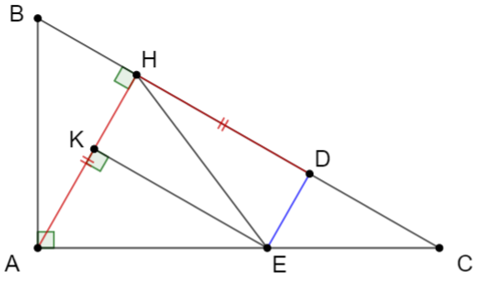
Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. a) Chứng minh ABH đồng dạng tam giác ABC. (ảnh 1)

a) Xét hai tam giác DABH và DCBA có

$\begin{matrix} \hat{A B H} = \hat{C B A} (\hat{B} c h u n g) \\ \hat{A H B} = \hat{C A B} (= 90 °) \end{matrix}\} \Rightarrow Δ A B H ∽ Δ C B A (g . g)$

Câu 3

c) Trên tia HC, lấy H = HA. Từ D vẽ đường thẳng song song AH cắt AC tại E.
Chứng minh AE = AB.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Một mảnh đất hình chữ nhật có chiều rộng kém chiều dài 5 m. Nếu tăng chiều dài lên 3m và tăng chiều rộng lên 2 m thì diện tích tăng thêm 41 m². Tính chu vi hình chữ nhật lúc ban đầu.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Giải các phương trình sau:

a) 5x - 2 = 3x + 4

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cô Phương giảm giá 30% cho một số nồi cơm điện tồn kho so với giá vốn ban đầu là 3 000 000 đồng/ cái. Bán được một số cái, cô Phương quyết định giảm giá thêm 10% nữa so với giá bán ban đầu cho những nồi còn lại. Biết cô Phương bán hết thu về 153 000 000 đồng. Hỏi cô Phương đã bán được bao nhiêu cái nồi cơm điện? Biết rằng số nồi cơm điện bán được sau lần giảm giá lần hai nhiều hơn lần đầu là 20 nồi.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

b) Chứng minh AH² = HB.HC.

Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH.
a) Chứng minh DABH đồng dạng DABC.

c) Trên tia HC, lấy H = HA. Từ D vẽ đường thẳng song song AH cắt AC tại E.
Chứng minh AE = AB.

Một mảnh đất hình chữ nhật có chiều rộng kém chiều dài 5 m. Nếu tăng chiều dài lên 3m và tăng chiều rộng lên 2 m thì diện tích tăng thêm 41 m². Tính chu vi hình chữ nhật lúc ban đầu.

Giải các phương trình sau:

a) 5x - 2 = 3x + 4