Một người thợ sử dụng thước ngắm có góc vuông để đo gián tiếp chiều cao của một cái cây. Với các kích thước đo được như hình bên: Khoảng cách từ vị trí gốc cây đến vị trí chân của người thợ là 2,25 m và từ vị trí chân đứng thẳng trên mặt đất đến mắt của người ngắm là 1,5 m. Hỏi với các kích thước trên thì người thợ đo được chiều cao của cây đó là bao nhiêu?
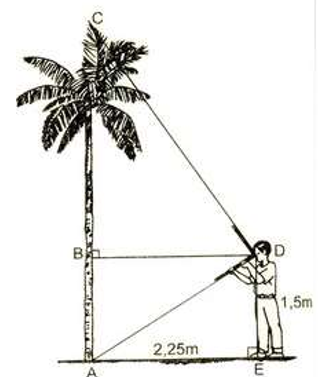
Một người thợ sử dụng thước ngắm có góc vuông để đo gián tiếp chiều cao của một cái cây. Với các kích thước đo được như hình bên: Khoảng cách từ vị trí gốc cây đến vị trí chân của người thợ là 2,25 m và từ vị trí chân đứng thẳng trên mặt đất đến mắt của người ngắm là 1,5 m. Hỏi với các kích thước trên thì người thợ đo được chiều cao của cây đó là bao nhiêu?
A. 3,25 m;
B. 4,875 m;
C. 5,625 m;
D. 4,5 m.
Câu hỏi trong đề: Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
Ta có:
+) AEDB là hình chữ nhật nên suy ra AB = DE = 1,5 m và BD = AE = 2,25 m
+) Áp dụng định lý Pytago vào tam giác AED vuông tại E có
+) Xét hai tam giác ABD và ADC có:
Vậy chiều cao của của cây đó là 4,875 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Gọi x (con) là số gà (x Î ℕ*)
Khi đó số chân gà là 2x (chân)
Tổng số con gà và bò là 1 200 con nên số con bò là 1200 − x (con)
Số chân bò là 4(1 200 – x) (chân)
Vì tổng số chân gà và chân bò là 2 700 chân nên ta có phương trình
2x + 4(1200 − x) = 2700
Û 2x + 4800 ‒ 4x = 2700
Û ‒2x = 2700 ‒ 4800
Û ‒2x = −2100
Û x = 1 050 (thỏa mãn)
Vậy số gà là 1 050 con và số bò là 1 200 ‒ 1050 = 150 (con).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
c) Áp dụng tính chất đường phân giác vào tam giác ACH có AK là đường phân giác
(4)
Từ (3) và (4) suy ra
Tam giác HAC có , áp dụng định lý Ta-lét đảo ta suy ra được:
IK // AC (đpcm).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. MN // BC;
B.
C.
D. DANM vuông.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập