Câu hỏi:
26/09/2022 4,431
Tính diện tích hình thoi \[MBND\]biết \[ABCD\] là hình vuông và hai đường chéo của hình vuông \[AC = BD = 20{\rm{ c}}m\]( \[M\]là điểm chính giữa AO; N là điểm chính giữa OC)
Tính diện tích hình thoi \[MBND\]biết \[ABCD\] là hình vuông và hai đường chéo của hình vuông \[AC = BD = 20{\rm{ c}}m\]( \[M\]là điểm chính giữa AO; N là điểm chính giữa OC)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Hai đường chéo hình vuông bằng nhau và cắt nhau tại trung điểm mỗi đường nên
\[OA = OC = 20:2 = 10(cm)\]
Vì điểm M, N là các điểm chính giữa của OA, OC nên:
\[OM = ON = OA:2 = 10:2 = 5(cm)\]
Do đó hình thoi \[MBND\] có độ dài đường chéo \[MN = 2.OM = 2.5 = 10(cm)\]
Đường chéo \[BD = 20(cm)\]
Diện tích hình thoi \[MBND\] là \[\frac{1}{2}MN.BD = \frac{1}{2}10.20 = 100(c{m^2})\]
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
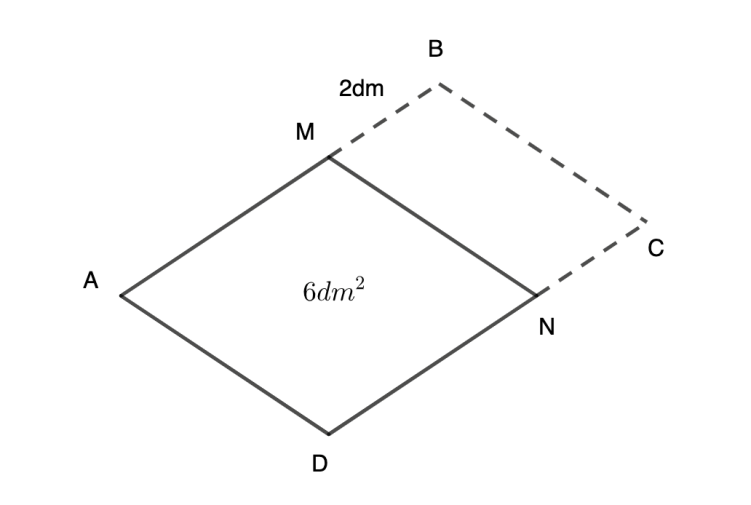
\[AMND\] là hình thoi nên \[AM = MN = DN = AD\]
\[ABCD\]là hình bình hành nên \[BC = AD\]
\[ \Rightarrow AM = BC = DN = AD\]
Chu vi hình bình hành là:
\[AM + BC + DN + AD + MB + NC = 4DN + 2MB = 2m = 20dm\]
\[ \Rightarrow 4DN + 2.2 = 20 \Rightarrow {\rm{4DN = 16}} \Rightarrow {\rm{DN = 4(dm)}}\]
Gọi h là độ dài đường cao của hình thoi AMND kẻ từ điểm M xuống cạnh DN
\[h = {S_{AMND}}:DN = 6:4 = 1,5(dm)\]
h đồng thời là độ dài đường cao của hình bình hành ABCD
Diện tích hình bình hành là: \[{S_{ABCD}} = CD.h = \left( {4 + 2} \right).1,5 = 9(d{m^2})\]
Lời giải
Lời giải
Độ dài đường chéo lớn là \[220:\left( {2 + 3} \right).3 = 132{\rm{ }}\left( m \right)\]
Độ dài đường chéo nhỏ là \[220 - 132{\rm{ = 88}}\left( m \right)\]
Diện tích mảnh vườn là \[\frac{1}{2} \cdot 132 \cdot 88 = 5808\left( {{m^2}} \right)\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
-
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
-
10 câu Trắc nghiệm Toán 6 Chân trời sáng tạo Bài 1: Tập hợp. Phần tử của tập hợp (có đáp án)
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 11
-
Dạng 1. Biểu diễn một tập hợp cho trước
-
Đề thi Toán 6 Học kì 2 có đáp án (Đề 11)