Câu hỏi:
11/07/2024 6,679
Tìm giá trị nguyên dương của x để đa thức x3 – 3x2 – 3x – 1 chia hết cho đa thức x2 + x + 1.
Tìm giá trị nguyên dương của x để đa thức x3 – 3x2 – 3x – 1 chia hết cho đa thức x2 + x + 1.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Thực hiện phép chia đa thức như sau:
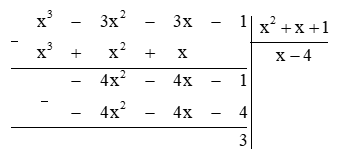
Để đa thức x3 – 3x2 – 3x – 1 chia hết cho đa thức x2 + x + 1 thì 3 ⋮ (x2 + x + 1).
Tức là x2 + x + 1 ∈ Ư(3) = {–3; 3; –1; 1}.
Do x > 0 nên x2 + x + 1 > 1
Do đó x2 + x + 1 = 3
x2 + x – 2 = 0
x2 – x + 2x – 2 = 0
x(x – 1) + 2(x – 1) = 0
(x – 1)(x + 2) = 0
Suy ra x = 1 (thỏa mãn) hoặc x = – 2 (loại).
Vậy x = 1 thì đa thức x3 – 3x2 – 3x – 1 chia hết cho đa thức x2 + x + 1.
Nhà sách vietjack
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.
So sánh các góc của tam giác ABC.
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.
So sánh các góc của tam giác ABC.
Xem đáp án »
11/07/2024
8,642
Câu 2:
Ba phân xưởng in có tổng cộng có 47 máy in (có cùng công suất in) và mỗi phân xưởng được giao in một số trang in bằng nhau. Phân xưởng thứ nhất hoàn thành công việc trong 3 ngày, phân xưởng thứ hai trong 4 ngày và phân cưởng thứ ba trong 5 ngày. Hỏi mỗi phân xưởng có bao nhiêu máy in?
Ba phân xưởng in có tổng cộng có 47 máy in (có cùng công suất in) và mỗi phân xưởng được giao in một số trang in bằng nhau. Phân xưởng thứ nhất hoàn thành công việc trong 3 ngày, phân xưởng thứ hai trong 4 ngày và phân cưởng thứ ba trong 5 ngày. Hỏi mỗi phân xưởng có bao nhiêu máy in?
Xem đáp án »
11/07/2024
8,340
Câu 3:
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.
Gọi I là trung điểm của CN. Chứng minh ba điểm B, M, I thẳng hàng.
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.
Gọi I là trung điểm của CN. Chứng minh ba điểm B, M, I thẳng hàng.
Xem đáp án »
11/07/2024
7,165
Câu 5:
Cho hai đa thức A(x) = x – 2x2 + 3x5 + x4 + x + x2;
B(x) = –2x2 + x – 2 – x4 + 3x2 – 3x5.
Tìm nghiệm của đa thức N(x) biết A(x) = N(x) – B(x).
Cho hai đa thức A(x) = x – 2x2 + 3x5 + x4 + x + x2;
B(x) = –2x2 + x – 2 – x4 + 3x2 – 3x5.
Tìm nghiệm của đa thức N(x) biết A(x) = N(x) – B(x).
Xem đáp án »
11/07/2024
3,164
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
Bộ 5 đề thi Giữa kì 2 Toán 7 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 01
-
Bộ 5 đề thi Giữa kì 2 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 01
-
12 Bài tập Một số bài toán thực tế liên quan đại lượng tỉ lệ thuận (có lời giải)
-
12 Bài tập Một số bài toán thực tế liên quan đại lượng tỉ lệ nghịch (có lời giải)
-
Bộ 5 đề thi Giữa kì 2 Toán 7 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 02
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận