Lấy điểm A trên $(O; R),$ vẽ tiếp tuyến $A x .$ Trên $A x,$ lấy điểm B, trên $(O; R)$ lấy điểm C sao cho $B C = A B .$
Lấy M trên cung nhỏ AC của (O) vẽ tiếp tuyến tại M cắt AB, BC lần lượt tại E,F. Vẽ đường tròn tâm I nội tiếp tam giác BFE. Chứng minh rằng: $Δ M A C ~ Δ I F E .$

Xem lời giải

Câu hỏi trong đề: Bộ 15 đề kiểm tra học kì 1 Toán 9 năm 2022-2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Kẻ đường kính CP của $(O; R)$

Ta có: $∠ P O A$ là góc ngoài của tam giác OAC nên $∠ P O A = ∠ O C A + ∠ O A C$ mà $∠ O A C = ∠ O C A$ (do tam giác OAC cân tại O) nên $∠ P O A = 2 ∠ A C O .$

Lại có $∠ P O M$ là góc ngoài của tam giác OCM nên $∠ P O M = ∠ O C M + ∠ O M C$ mà $∠ O C M = ∠ O M C$ (do tam giác OCM cân tại O) nên $∠ P O M = 2 ∠ M C O .$

Do đó: $∠ P O M - ∠ P O A = 2 (∠ M C O - ∠ A C O)$ hay $∠ M O A = 2 ∠ M C A .$

Xét tứ giác EMOA có $∠ E A O = ∠ E M O = 90 °$ (tính chất tiếp tuyến)

Nên $∠ M O A + ∠ A E M = 360 ° - (∠ E A O + ∠ E M O) = 180 °$

Mà $∠ A E M + ∠ B E F = 180 °$ (hai góc kề bù)

Nên $∠ M O A = ∠ B E F$ (cùng bù với $∠ A E M$ )

Lại có $∠ B E F = 2 ∠ I E F$ (do I là tâm đường tròn nội tiếp tam giác BEF)

Và $∠ M O A = 2 ∠ M C A (c m t)$

Suy ra $∠ I E F = ∠ M C A$

Chứng minh tương tự:

Ta có $∠ D O M$ là góc ngoài của tam giác cân $A O M \Rightarrow ∠ D O M = 2 ∠ M A O$

$∠ D O C$ là góc ngoài của tam giác cân $A O C \Rightarrow ∠ D O C = 2 ∠ C A O$

Trừ vế với vế ta được: $∠ M O C = 2 ∠ M A C$

Lại có $∠ M F C + ∠ M O C = 360 ° - (∠ F M O - ∠ C F O) = 180 °$

Và $∠ M F C + ∠ B F E = 180 ° \Rightarrow ∠ B F E = ∠ C O M$

Mà $∠ C O M = 2 ∠ M A C; ∠ B F E = 2 ∠ I F E$ nên $∠ I F E = ∠ M A C$

Xét tam giác IEF và tam giác MCA có: $∠ I F E = ∠ M A C$ và $∠ I E F = ∠ M C A (c m t)$ nên $Δ I E F$ đồng dạng với $Δ M C A$ (đpcm).

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hai biểu thức: $A = \frac{x + 7}{3 \sqrt{x}}$ và $B = \frac{2 \sqrt{x}}{\sqrt{x} + 3} + \frac{\sqrt{x} + 1}{\sqrt{x} - 3} + \frac{7 \sqrt{x} + x}{9 - x}$ với $x > 0; x \neq 9$

Tính giá trị nhỏ nhất của biểu thức P=A.B

Xem đáp án

Lời giải

Điều kiện xác định: $x > 0; x \neq 9$

$P = A . B = \frac{x + 7}{3 \sqrt{x}} . \frac{3 \sqrt{x}}{\sqrt{x} + 3} = \frac{x + 7}{\sqrt{x} + 3} = \frac{x - 9 + 16}{\sqrt{x} + 3} = \frac{(\sqrt{x} - 3) (\sqrt{x} + 3)}{\sqrt{x} + 3} + \frac{16}{\sqrt{x} + 3} = \sqrt{x} - 3 + \frac{16}{\sqrt{x} + 3} = (\sqrt{x} + 3) + \frac{16}{\sqrt{x} + 3} - 6$

Với mọi $x > 0, x \neq 9$ ta có: $\sqrt{x} + 3 > 0; \frac{16}{\sqrt{x} + 3} > 0.$

Áp dụng BĐT Cô-si cho hai số dương $(\sqrt{x} + 3)$ và $\frac{16}{\sqrt{x} + 3}$ ta có:

$(\sqrt{x} + 3) + \frac{16}{\sqrt{x} + 3} \geq 2 \sqrt{(\sqrt{x} + 3) . \frac{16}{\sqrt{x} + 3}} \Leftrightarrow (\sqrt{x} + 3) + \frac{16}{\sqrt{x} + 3} \geq 8 \Leftrightarrow (\sqrt{x} + 3) + \frac{16}{\sqrt{x} + 3} - 6 \geq 2$

Hay $P \geq 2.$

Dấu “=” xảy ra khi $\sqrt{x} + 3 = \frac{16}{\sqrt{x} + 3} \Rightarrow {(\sqrt{x} + 3)}^{2} = 16$

$\Leftrightarrow [\begin{array}{l} \sqrt{x} + 3 = 4 \\ \sqrt{x} + 3 = - 4 (k t m) \end{array} \Rightarrow \sqrt{x} = 1 \Leftrightarrow x = 1 (t m)$

Vậy giá trị nhỏ nhất của P là $2 \Leftrightarrow x = 1.$

Câu 2

Cho đường thẳng $(d_{1}) : y = 2 x + 2.$

Vẽ đường thẳng $(d_{1})$ trên mặt phẳng tọa độ Oxy

Xem đáp án

Lời giải

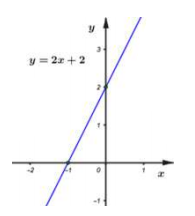
Media VietJack

Cho $x = 0 \Rightarrow y = 2$

$y = 0 \Rightarrow x = - 1$

Đồ thị hàm số $y = 2 x + 2$ là đường thẳng đi qua hai điểm có tọa độ $(0; 2)$ và $(- 1; 0)$

Câu 3