Cho đường tròn (O; R) và một điểm S nằm bên ngoài đường tròn. Kẻ các tiếp tuyến SA, SB với đường tròn (A, B là các tiếp điểm). Một đường thẳng đi qua S (không đi qua tâm O) cắt đường tròn (O; R) tại hai điểm M và N với M nằm giữa S và N. Gọi H là giao điểm của SO và AB; I là trung điểm MN. Hai đường thẳng OI và AB cắt nhau tại E.
a) Chứng minh IHSE là tứ giác nội tiếp đường tròn.
Cho đường tròn (O; R) và một điểm S nằm bên ngoài đường tròn. Kẻ các tiếp tuyến SA, SB với đường tròn (A, B là các tiếp điểm). Một đường thẳng đi qua S (không đi qua tâm O) cắt đường tròn (O; R) tại hai điểm M và N với M nằm giữa S và N. Gọi H là giao điểm của SO và AB; I là trung điểm MN. Hai đường thẳng OI và AB cắt nhau tại E.
a) Chứng minh IHSE là tứ giác nội tiếp đường tròn.Câu hỏi trong đề: Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
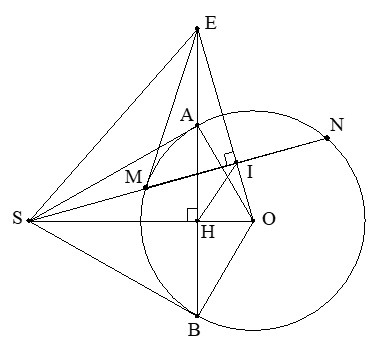
a) Chứng minh tứ giác IHSE nội tiếp trong một đường tròn :
Ta có SA = SB ( tính chất của tiếp tuyến)
Nên SAB cân tại S
Do đó tia phân giác SO cũng là đường cao => SOAB
I là trung điểm của MN nên OI MN
Do đó
=> Hai điểm H và I cùng nhìn đoạn SE dưới 1 góc vuông nên tứ giác IHSE nội tiếp đường tròn đường kính SEĐăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi vận tốc của xe khách là x (km/h). ĐK : x > 0
Vận tốc của xe du lịch là : x + 20 (km/h)
Thời gian xe khách đi hết AB là:
Thời gian xe du lịch đi hết AB là:
50 phút = giờ
Theo đề bài ta có phương trình:
Giải phương trình ta được: x1 = 40 (Nhận)
x2 = - 60 (Loại)
Trả lời: Vận tốc của xe khách là 40 km/h
Vận tốc của xe du lịch là 60 km/hĐăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
b) SOI ~ EOH ( g.g)
mà OH.OS = OB2 = R2 ( hệ thức lượng trong tam giác vuông SOB)
nên OI.OE = R2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập