Từ một điểm S ở ngoài đường tròn (O) kẻ tiếp tuyến SA và cát tuyến SBC với đường tròn (O).Một đường thẳng song song với SA cắt dây AB, AC lần lược tại N,M
1) Chứng minh : Tam giác AMN đồng dạng với tam giác ABC
2) Chứng minh : là tứ giác nội tiếp.
3) Vẽ phân giác của góc BAC cắt dây BC tại . Chứng minh:
4) Trên dây AC lấy điểm Esao choChứng minh : AOvuông góc với DE
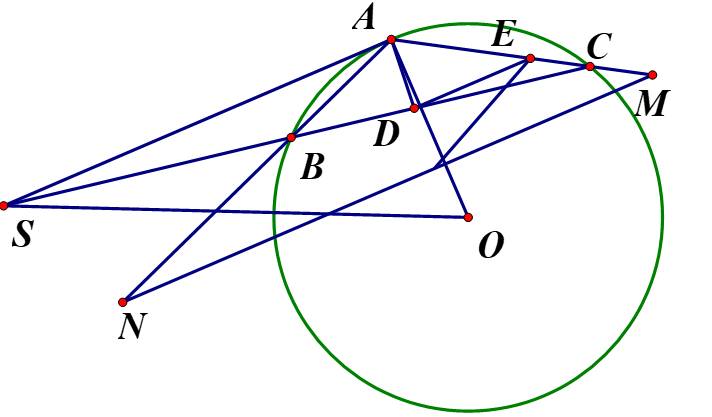
Từ một điểm S ở ngoài đường tròn (O) kẻ tiếp tuyến SA và cát tuyến SBC với đường tròn (O).Một đường thẳng song song với SA cắt dây AB, AC lần lược tại N,M
1) Chứng minh : Tam giác AMN đồng dạng với tam giác ABC
2) Chứng minh : là tứ giác nội tiếp.
3) Vẽ phân giác của góc BAC cắt dây BC tại . Chứng minh:
4) Trên dây AC lấy điểm Esao choChứng minh : AOvuông góc với DE
Quảng cáo
Trả lời:
Giải bởi Vietjack
a)
Do là hai tiếp tuyến, cát tuyến của (O) nên nội tiếp (O) (cùng chắn cung
Xét và có:
b) Xét tứ giác có: và
Mà đối nhau nên là tứ giác nội tiếp
c) Xét và có : chung,
Do AD là phân giác của nên :
(tính chất phân giác ) (2)
Từ (1) và (2) suy ra
Xét có:
Mà (phân giác)
cân tại S
d) Tứ giác nội tiếp nên (cùng nhìn cung AB)
Mà cân)mà 2 góc ở vị trí so le trong
Nên mà (tính chất tiếp tuyến )
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
2, Vì
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập