Câu hỏi:
10/03/2023 671
Gọi a, b, c lần lượt là ba cạnh của tam giác; ha, hb, hc lần lượt là các đường cao tương ứng với ba cạnh đó và r là bán kính đường tròn nội tiếp tam giác đó. Chứng minh rằng: \(\frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}} = \frac{1}{r}\).
Gọi a, b, c lần lượt là ba cạnh của tam giác; ha, hb, hc lần lượt là các đường cao tương ứng với ba cạnh đó và r là bán kính đường tròn nội tiếp tam giác đó. Chứng minh rằng: \(\frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}} = \frac{1}{r}\).
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
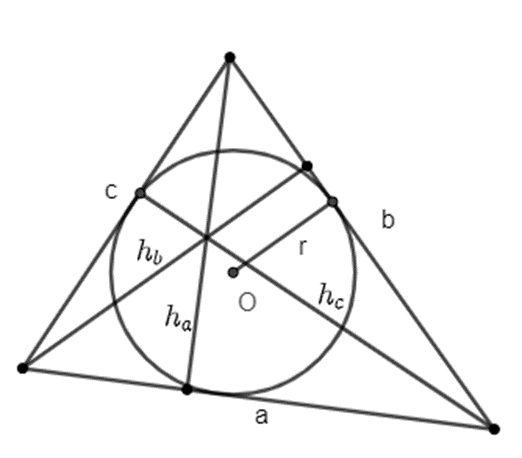
Ta có:
\(S = \frac{1}{2}a.{h_a} \Rightarrow \frac{1}{{{h_a}}} = \frac{a}{{2S}}\);
\(S = \frac{1}{2}b.{h_b} \Rightarrow \frac{1}{{{h_b}}} = \frac{b}{{2S}}\);
\(S = \frac{1}{2}c.{h_c} \Rightarrow \frac{1}{{{h_c}}} = \frac{c}{{2S}}\).
Do đó: \(\frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}} = \frac{{a + b + c}}{{2S}} = \frac{{2p}}{{2S}} = \frac{p}{S} = \frac{p}{{p.r}} = \frac{1}{r}\).
Hay \(\frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}} = \frac{1}{r}\) (đpcm).
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Ông và bà An cùng có 6 đứa con đang lên máy bay theo một hàng dọc. Có bao nhiêu cách xếp hàng khác nhau nếu ông hay bà An đứng ở đầu hoặc cuối hàng.
Ông và bà An cùng có 6 đứa con đang lên máy bay theo một hàng dọc. Có bao nhiêu cách xếp hàng khác nhau nếu ông hay bà An đứng ở đầu hoặc cuối hàng.
Xem đáp án »
10/03/2023
17,268
Câu 2:
Một lớp học có 25 học sinh học khá các môn tự nhiên, 24 học sinh học khá các môn xã hội, 10 học sinh học khá cả môn tự nhiên lẫn môn xã hội, đặc biệt vẫn còn 3 học sinh chưa học khá cả hai nhóm môn ấy. Hỏi lớp có bao nhiêu học sinh chỉ khá đúng một nhóm môn (tự nhiên hoặc xã hội).
Một lớp học có 25 học sinh học khá các môn tự nhiên, 24 học sinh học khá các môn xã hội, 10 học sinh học khá cả môn tự nhiên lẫn môn xã hội, đặc biệt vẫn còn 3 học sinh chưa học khá cả hai nhóm môn ấy. Hỏi lớp có bao nhiêu học sinh chỉ khá đúng một nhóm môn (tự nhiên hoặc xã hội).
Xem đáp án »
10/03/2023
9,593
Câu 3:
Cho hai tập hợp khác rỗng: A = (m – 1; 4], B = (−2; 2m + 2), với m ∈ ℝ. Xác định m để:
a) A ∩ B = Ø;
b) A ⊂ B;
c) B ⊂ A;
d) (A ∩ B) ⊂ (−1; 3).
Cho hai tập hợp khác rỗng: A = (m – 1; 4], B = (−2; 2m + 2), với m ∈ ℝ. Xác định m để:
a) A ∩ B = Ø;
b) A ⊂ B;
c) B ⊂ A;
d) (A ∩ B) ⊂ (−1; 3).
Xem đáp án »
10/03/2023
5,361
Câu 4:
Một liên đoàn bóng rổ có 10 đội, mỗi đội đấu với mỗi đội khác 2 lần, một lần ở sân nhà và một lần ở sân khách. Số trận đấu được sắp xếp là bao nhiêu?
Một liên đoàn bóng rổ có 10 đội, mỗi đội đấu với mỗi đội khác 2 lần, một lần ở sân nhà và một lần ở sân khách. Số trận đấu được sắp xếp là bao nhiêu?
Xem đáp án »
10/03/2023
4,998
Câu 5:
Một bó hoa 12 bông gồm: 5 hoa hồng, 4 hoa lan còn lại là hoa cúc. Chọn ngẫu nhiên 5 bông hoa. Tính xác suất sao cho chọn đủ ba loại và số cúc không ít hơn 2.
Một bó hoa 12 bông gồm: 5 hoa hồng, 4 hoa lan còn lại là hoa cúc. Chọn ngẫu nhiên 5 bông hoa. Tính xác suất sao cho chọn đủ ba loại và số cúc không ít hơn 2.
Xem đáp án »
10/03/2023
4,873
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận