Câu hỏi:
13/07/2024 964
Cho mạch điện: U = 16V , R0 =4 Ω , R1 = 12 Ω, Rx là giá trị tức thời của một biến trở đủ lớn, ampe kế A và dây nối có điện trở không đáng kể.
1. Tính Rx sao cho công suất tiêu thụ trên nó bằng 9 W và tính hiệu suất của mạch điện. Biết rằng tiêu hao năng lượng trên R1, Rx là có ích, trên R0 là vô ích.
2. Với giá trị nào của Rx thì công suất tiêu thụ trên nó là cực đại? Tính công suất ấy?
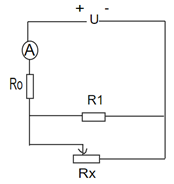
Cho mạch điện: U = 16V , R0 =4 Ω , R1 = 12 Ω, Rx là giá trị tức thời của một biến trở đủ lớn, ampe kế A và dây nối có điện trở không đáng kể.
1. Tính Rx sao cho công suất tiêu thụ trên nó bằng 9 W và tính hiệu suất của mạch điện. Biết rằng tiêu hao năng lượng trên R1, Rx là có ích, trên R0 là vô ích.
2. Với giá trị nào của Rx thì công suất tiêu thụ trên nó là cực đại? Tính công suất ấy?
Câu hỏi trong đề:
2020 câu Trắc nghiệm tổng hợp Vật lí 2023 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Mạch: \({R_0}nt\left( {{R_1}//R{}_x} \right)\)
Đặt Rx = x \(\left( \Omega \right)\)
\({R_{td}} = {R_0} + \frac{{{R_1}.x}}{{{R_1} + x}} = 4 + \frac{{12x}}{{12 + x}} = \frac{{16x + 48}}{{12 + x}}\)
\( \Rightarrow I = \frac{U}{{{R_{td}}}} = \frac{{16}}{{\frac{{16x + 48}}{{12 + x}}}} = \frac{{12 + x}}{{x + 3}}\)
\({U_{Rx}} = U{}_{R1} = U{}_{R1x} = \frac{{12 + x}}{{x + 3}}.\frac{{12x}}{{12 + x}} = \frac{{12x}}{{x + 3}}\)
Mà \(P = \frac{{U_{Rx}^2}}{{{R_x}}} = 9W \Leftrightarrow \frac{{\frac{{144{x^2}}}{{{{\left( {x + 3} \right)}^2}}}}}{x} = 9 \Rightarrow 9{x^2} - 90x + 81 = 0\)
\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = 1 \Rightarrow {R_x} = 1\left( \Omega \right)}\\{x = 9 \Rightarrow {R_x} = 9\left( \Omega \right)}\end{array}} \right.\)
Hiệu suất của mạch điện
\(H = \frac{{{P_{1x}}}}{P}.100\% = \frac{{{I^2}.{R_{1x}}}}{{{I^2}.{R_{td}}}}.100\% = \frac{{{R_{1x}}}}{{{R_{td}}}}.100\% = \frac{{3{R_x}}}{{4{R_x} + 12}}.100\% \)
+ Rx = 1\(\left( \Omega \right)\) \( \Rightarrow H = 18,75\% \)
+ Rx = 9\(\left( \Omega \right)\) \( \Rightarrow H = 56,25\% \)
b. Từ câu a
\( \Rightarrow {P_{{R_x}}} = \frac{{{U^2}}}{{{R_x}}} = \frac{{{{\left( {\frac{{12x}}{{x + 3}}} \right)}^2}}}{x} = \frac{{144x}}{{{x^2} + 6x + 9}} = \frac{{144}}{{x + \frac{9}{x} + 6}}\)
Để PRx max khi \((x + \frac{9}{x} + 6)\,\,\min \)\( \Rightarrow \left( {x + \frac{9}{x}} \right)\,\,\min \)
Áp dụng BĐT Cô – si: \(x + \frac{9}{x} \ge 2\sqrt {x.\frac{9}{x}} = 6\)
\( \Rightarrow {P_{Rx\,max}} = \frac{{144}}{{6 + 6}} = 12\,\left( W \right)\)Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một ca nô chạy trong hồ nước yên lặng có vận tốc tối đa 18 km/h. Nếu ca nô chạy ngang một con sông có dòng chảy theo hướng Bắc – Nam với vận tốc lên tới 5 m/s thì vận tốc tối đa nó có thể đạt được so với bờ sông là bao nhiêu và theo hướng nào?
Xem đáp án »
03/04/2023
47,870
Câu 2:
Tại hai điểm A và B trên mặt nước có hai nguồn sóng giống nhau với biên độ a, bước sóng là 10 cm. Điểm N cách A một khoảng 25 cm, cách B một khoảng 10 cm sẽ dao động với biên độ là
Xem đáp án »
04/04/2023
38,533
Câu 3:
Hai xe I và II chuyển động trên cùng một đường thẳng tại hai điểm A và B. Biết tốc độ xe I và xe II lần lượt là 50 km/h và 30 km/h. Tính vận tốc tương đối của xe I so với xe II khi:
a) Hai xe chuyển động cùng chiều.
b) Hai xe chuyển động ngược chiều.
Hai xe I và II chuyển động trên cùng một đường thẳng tại hai điểm A và B. Biết tốc độ xe I và xe II lần lượt là 50 km/h và 30 km/h. Tính vận tốc tương đối của xe I so với xe II khi:
a) Hai xe chuyển động cùng chiều.
b) Hai xe chuyển động ngược chiều.
Xem đáp án »
04/04/2023
24,464
Câu 4:
Thả một hòn đá từ mép một vách núi dựng đứng xuống vực sâu. Sau 3,96 s từ lúc thả thì nghe thấy tiếng hòn đá chạm đáy vực sâu. Biết g = 9,8 m/s2 và tốc độ truyền âm trong không khí là 330 m/s. Tìm chiều cao vách đá bờ vực đó.
Xem đáp án »
03/04/2023
21,941
Câu 5:
Hai gương phẳng G1, G2 quay mặt phản xạ vào nhau và tạo với nhau một góc 600. Một điểm S nằm trong khoảng 2 gương.
a. Hãy nêu cách vẽ đường đi của tia sáng phát ra từ S phản xạ lần lượt qua G1, G2 rồi quay trở lại S.
b. Tính góc tạo bởi tia xuất phát từ S và tia phản xạ đi qua S.
Hai gương phẳng G1, G2 quay mặt phản xạ vào nhau và tạo với nhau một góc 600. Một điểm S nằm trong khoảng 2 gương.
a. Hãy nêu cách vẽ đường đi của tia sáng phát ra từ S phản xạ lần lượt qua G1, G2 rồi quay trở lại S.
b. Tính góc tạo bởi tia xuất phát từ S và tia phản xạ đi qua S.
Xem đáp án »
04/04/2023
16,357
Câu 6:
Một người kéo một thùng nước có khối lượng 12 kg từ giếng sâu 8 m. Lấy g = 10 m/s2.
a) Tính công và công suất của người khi kéo đều thùng nước hết 16 s.
b) Nếu dùng máy để kéo thùng nước nói trên đi lên nhanh dần đều và thời gian kéo mất 2 s thì công và công suất của máy bằng bao nhiêu?
Một người kéo một thùng nước có khối lượng 12 kg từ giếng sâu 8 m. Lấy g = 10 m/s2.
a) Tính công và công suất của người khi kéo đều thùng nước hết 16 s.
b) Nếu dùng máy để kéo thùng nước nói trên đi lên nhanh dần đều và thời gian kéo mất 2 s thì công và công suất của máy bằng bao nhiêu?
Xem đáp án »
04/04/2023
14,894
Câu 7:
Tính lực tương tác điện, lực hấp dẫn giữa electron và hạt nhân trong nguyên tử Hyđrô. Biết khoảng cách giữa chúng là 5.10-9 cm, khối lượng hạt nhân bằng 1836 lần khối lượng electron.
Xem đáp án »
04/04/2023
14,197
về câu hỏi!