Câu hỏi:
04/04/2023 16,369
Một vật khối lượng m = 1 kg được kéo chuyển động ngang bởi một lực \(\vec F\) hợp với phương ngang một góc \(\alpha \)= 30° và có độ lớn F = 2 N. Biết khi bắt đầu chuyển động được 2 s vật đi được quãng đường 1,66 m. Cho g = 10 m/s2, \(\sqrt 3 = 1,73\).
a, Tính hệ số ma sát trượt giữa vật và mặt sàn.
b, Tính hệ số ma sát với lực kéo nói trên vật chuyển động thẳng đều.
Một vật khối lượng m = 1 kg được kéo chuyển động ngang bởi một lực \(\vec F\) hợp với phương ngang một góc \(\alpha \)= 30° và có độ lớn F = 2 N. Biết khi bắt đầu chuyển động được 2 s vật đi được quãng đường 1,66 m. Cho g = 10 m/s2, \(\sqrt 3 = 1,73\).
a, Tính hệ số ma sát trượt giữa vật và mặt sàn.
b, Tính hệ số ma sát với lực kéo nói trên vật chuyển động thẳng đều.
Câu hỏi trong đề: 2020 câu Trắc nghiệm tổng hợp Vật lí 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
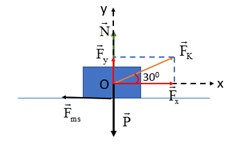
Chọn hệ trục Oxy như hình vẽ.
Vật chịu tác dụng của các lực \(\vec F,\,{\vec F_{ms}},\vec N,\,\vec P\)
Theo định luật II Newton, ta có: \(\vec F + {\vec F_{ms}} + \vec N + \vec P = m.\vec a\)
Chiếu lần lượt lên Ox, Oy, ta được:
\(\left\{ {\begin{array}{*{20}{c}}{{F_x} - {F_{ms}} = m.a \Rightarrow {F_x} - \mu .N = m.a\,(1)}\\{{F_y} + N - P = 0 \Rightarrow N = P - F{}_y\,(2)}\end{array}} \right.\)
Thay (2) vào (1), được:
\(F.cos{30^0} - \mu \left( {P - F.\sin {{30}^0}} \right) = m.a\,\,\left( 3 \right)\)
Lại có: \(s = {v_0}.t + \frac{1}{2}a.{t^2} \Rightarrow a = \frac{{2s}}{{{t^2}}} = \frac{{2.1,66}}{{{2^2}}} = 0,83\,m/{s^2}\)
Thay vào (3) \( \Rightarrow \mu = \frac{{F.cos{{30}^0} - m.a}}{{P - F.\sin {{30}^0}}} = \frac{{2.\frac{{\sqrt 3 }}{2} - 1.0,83}}{{1.10 - 2.0,5}} \approx 0,1\)
b. Khi vật chuyển động thẳng đều thì a = 0
\( \Rightarrow \mu = \frac{{F.cos{{30}^0} - m.a}}{{P - F.\sin {{30}^0}}} = \frac{{2.\frac{{\sqrt 3 }}{2} - 1.0}}{{1.10 - 2.0,5}} \approx 0,192\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tại hai điểm A và B trên mặt nước có hai nguồn sóng giống nhau với biên độ a, bước sóng là 10 cm. Điểm N cách A một khoảng 25 cm, cách B một khoảng 10 cm sẽ dao động với biên độ là
Xem đáp án »
04/04/2023
53,916
Câu 2:
Một ca nô chạy trong hồ nước yên lặng có vận tốc tối đa 18 km/h. Nếu ca nô chạy ngang một con sông có dòng chảy theo hướng Bắc – Nam với vận tốc lên tới 5 m/s thì vận tốc tối đa nó có thể đạt được so với bờ sông là bao nhiêu và theo hướng nào?
Xem đáp án »
03/04/2023
51,544
Câu 3:
Một người kéo một thùng nước có khối lượng 12 kg từ giếng sâu 8 m. Lấy g = 10 m/s2.
a) Tính công và công suất của người khi kéo đều thùng nước hết 16 s.
b) Nếu dùng máy để kéo thùng nước nói trên đi lên nhanh dần đều và thời gian kéo mất 2 s thì công và công suất của máy bằng bao nhiêu?
Một người kéo một thùng nước có khối lượng 12 kg từ giếng sâu 8 m. Lấy g = 10 m/s2.
a) Tính công và công suất của người khi kéo đều thùng nước hết 16 s.
b) Nếu dùng máy để kéo thùng nước nói trên đi lên nhanh dần đều và thời gian kéo mất 2 s thì công và công suất của máy bằng bao nhiêu?
Xem đáp án »
04/04/2023
33,260
Câu 4:
Thả một hòn đá từ mép một vách núi dựng đứng xuống vực sâu. Sau 3,96 s từ lúc thả thì nghe thấy tiếng hòn đá chạm đáy vực sâu. Biết g = 9,8 m/s2 và tốc độ truyền âm trong không khí là 330 m/s. Tìm chiều cao vách đá bờ vực đó.
Xem đáp án »
03/04/2023
33,009
Câu 5:
Hai gương phẳng G1, G2 quay mặt phản xạ vào nhau và tạo với nhau một góc 600. Một điểm S nằm trong khoảng 2 gương.
a. Hãy nêu cách vẽ đường đi của tia sáng phát ra từ S phản xạ lần lượt qua G1, G2 rồi quay trở lại S.
b. Tính góc tạo bởi tia xuất phát từ S và tia phản xạ đi qua S.
Hai gương phẳng G1, G2 quay mặt phản xạ vào nhau và tạo với nhau một góc 600. Một điểm S nằm trong khoảng 2 gương.
a. Hãy nêu cách vẽ đường đi của tia sáng phát ra từ S phản xạ lần lượt qua G1, G2 rồi quay trở lại S.
b. Tính góc tạo bởi tia xuất phát từ S và tia phản xạ đi qua S.
Xem đáp án »
04/04/2023
31,472
Câu 6:
Hai xe I và II chuyển động trên cùng một đường thẳng tại hai điểm A và B. Biết tốc độ xe I và xe II lần lượt là 50 km/h và 30 km/h. Tính vận tốc tương đối của xe I so với xe II khi:
a) Hai xe chuyển động cùng chiều.
b) Hai xe chuyển động ngược chiều.
Hai xe I và II chuyển động trên cùng một đường thẳng tại hai điểm A và B. Biết tốc độ xe I và xe II lần lượt là 50 km/h và 30 km/h. Tính vận tốc tương đối của xe I so với xe II khi:
a) Hai xe chuyển động cùng chiều.
b) Hai xe chuyển động ngược chiều.
Xem đáp án »
04/04/2023
27,960
🔥 Đề thi HOT:
-
83 câu Trắc nghiệm Vật lý 12 Cánh diều Chủ đề 4: Vật lý hạt nhân
-
56 câu Trắc nghiệm Vật lý 12 Cánh diều Chủ đề 2: Khí lý tưởng
-
1000 câu hỏi lý thuyết trọng tâm môn Vật Lý lớp 12 có đáp án
-
62 câu Trắc nghiệm Vật lý 12 Cánh diều Chủ đề 3: Từ trường có đáp án
-
91 câu Trắc nghiệm Vật lý 12 Cánh diều Chủ đề 1: Vật lý nhiệt
-
21 câu Trắc nghiệm Vật lý 12 Kết nối tri thức Bài 1. Cấu trúc của chất. Sự chuyển thể có đáp án
-
2020 câu Trắc nghiệm tổng hợp Vật lí 2023 có đáp án (Phần 2)
-
21 câu Trắc nghiệm Vật lý 12 Kết nối tri thức Bài 2. Nội năng. Định luật I của nhiệt động lực học có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận