Câu hỏi:

19/08/2025 1,647

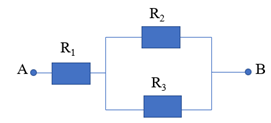
Có mạch điện như hình vẽ: \({R_1} = 8\Omega ;\,{R_2} = 6\Omega ;\,{R_3} = 12\Omega \). Hiệu điện thế U_AB = 24 V.

a. Tính cường độ dòng điện qua mỗi điện trở.

b. Tính công suất tỏa nhiệt của đoạn mạch.

c. Tính nhiệt lượng tỏa ra của điện trở R₃ trong thời gian 10 phút.

Xem lời giải

Câu hỏi trong đề: 2020 câu Trắc nghiệm tổng hợp Vật lí 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải

Mạch: R₁ nt (R₂ // R₃)

\({R_{23}} = \frac{{{R_2}.{R_3}}}{{{R_2} + {R_3}}} = \frac{{6.12}}{{6 + 12}} = 4\Omega \)

\({R_{123}} = {R_1} + {R_{23}} = 8 + 4 = 12\Omega \)

a. Cường độ dòng điện mạch chính là

\(I = \frac{{{U_{AB}}}}{{{R_{123}}}} = \frac{{24}}{{12}} = 2A\)

Cường độ dòng điện qua R₁là

I₁ = I = 2 A

Mà I₂₃ = I = I₂ + I₃ = 2A

U₂ = U₃ = U₂₃ = I₂₃ . R₂₃ = 2. 4 = 8V

Cường độ dòng điện qua điện trở R₂ là

\({I_2} = \frac{{{U_2}}}{{R{}_2}} = \frac{8}{6} = \frac{4}{3}A\)

Cường độ dòng điện qua điện trở R₃ là

I₃ = I₂₃ – I₂ = \(2 - \frac{4}{3} = \frac{2}{3}A\)

b. Công suất tỏa nhiệt của đoạn mạch là

\({\rm{P}} = {I^2}.{R_{123}} = {2^2}.12 = 48W\)

c. Nhiệt lượng tỏa ra của điện trở R₃ trong thời gian 10 phút là

\({Q_3} = I_3^2.{R_3}.t = {\left( {\frac{2}{3}} \right)^2}.12.10.60 = 3200J\)

Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một ca nô chạy trong hồ nước yên lặng có vận tốc tối đa 18 km/h. Nếu ca nô chạy ngang một con sông có dòng chảy theo hướng Bắc – Nam với vận tốc lên tới 5 m/s thì vận tốc tối đa nó có thể đạt được so với bờ sông là bao nhiêu và theo hướng nào?

A. \(5\sqrt 2 \)m/s, hướng 45^o Đông – Nam.

B. \(5\sqrt 2 \)m/s, hướng 45^o Đông – Nam.

C. \(5\sqrt 2 \)m/s, hướng 45^o Đông – Bắc.

D. \(5\sqrt 2 \)m/s, hướng 45^o Đông – Bắc.

Lời giải

Đáp án đúng: B

Gọi v₁₃ là vận tốc của ca nô so với bờ sông, v₂₃ là vận tốc của nước so với bờ, v₁₂ là vận tốc của ca nô so với dòng nước.

Đổi v = 18 km/h = 5 m/s

Ca nô sẽ đi theo hướng Đông Nam so với bờ sông với vận tốc tối đa nó có thể đạt được là: \({v_{13}} = \sqrt {{v_{12}}^2 + v_{23}^2} = \sqrt {{5^2} + {5^2}} = 5\sqrt 2 \)(m/s)

Câu 2

Tại hai điểm A và B trên mặt nước có hai nguồn sóng giống nhau với biên độ a, bước sóng là 10 cm. Điểm N cách A một khoảng 25 cm, cách B một khoảng 10 cm sẽ dao động với biên độ là

A. 2a.

B. a.

C. – 2a.

D. 0.

Lời giải

Đáp án đúng: D

Hai nguồn sóng giống nhau tức là có độ lệch pha △φ = 0.

Biên độ sóng tại N là

\({A_N} = 2a\left| {cos\left( {\pi \frac{{NB - NA}}{\lambda }} \right)} \right| = 2a\left| {cos\left( {\pi \frac{{10 - 25}}{{10}}} \right)} \right| = 2a\left| {cos\frac{{\left( { - 3\pi } \right)}}{2}} \right| = 0\)

Câu 3

Thả một hòn đá từ mép một vách núi dựng đứng xuống vực sâu. Sau 3,96 s từ lúc thả thì nghe thấy tiếng hòn đá chạm đáy vực sâu. Biết g = 9,8 m/s² và tốc độ truyền âm trong không khí là 330 m/s. Tìm chiều cao vách đá bờ vực đó.

A. 76 m.

B. 58 m.

C. 69 m.

D. 82 m.

Lời giải