Câu hỏi:
11/04/2023 462
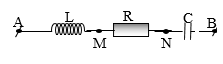
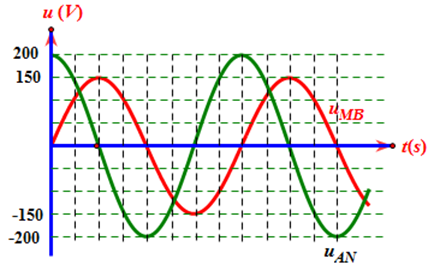
Đoạn mạch \[AB\] không phân nhánh gồm điện trở thuần R. cuộn thuần cảm có độ tự cảm L và tụ điện có điện dung C. Khi đặt vào hai dầu đoạn mạch AB điện áp \[{\user2{u}_\user2{1}}\user2{ = U}\sqrt 2 \;\user2{cos(50\pi t)(V)}\] thì công suất tiêu thụ của đoạn mạch là \[{P_1}\] vả hệ số công suất là \[{k_1}\]. Khi đặt vào hai đầu đoạn mạch \[AB\] điện áp \[{\user2{u}_2}\user2{ = 2U}\sqrt 2 \;\user2{cos(100\pi t)(V)}\] thì công suất tiêu thụ của đoạn mạch là \[{P_2} = 4{P_1}\] . Khi đặt vào hai đầu đoạn mạch \[AB\] điện áp \[{\user2{u}_3}\user2{ = 3U}\sqrt 2 \,\user2{cos(150\pi t)(V)}\] thì công suất tiêu thụ cùa đoạn mạch là \[{P_3} = \frac{{81}}{{13}}{P_1},\]và hệ số công suất là \[{k_3}\]. Giá trị\[{k_1}\];\[{k_3}\]gần bằng
Đoạn mạch \[AB\] không phân nhánh gồm điện trở thuần R. cuộn thuần cảm có độ tự cảm L và tụ điện có điện dung C. Khi đặt vào hai dầu đoạn mạch AB điện áp \[{\user2{u}_\user2{1}}\user2{ = U}\sqrt 2 \;\user2{cos(50\pi t)(V)}\] thì công suất tiêu thụ của đoạn mạch là \[{P_1}\] vả hệ số công suất là \[{k_1}\]. Khi đặt vào hai đầu đoạn mạch \[AB\] điện áp \[{\user2{u}_2}\user2{ = 2U}\sqrt 2 \;\user2{cos(100\pi t)(V)}\] thì công suất tiêu thụ của đoạn mạch là \[{P_2} = 4{P_1}\] . Khi đặt vào hai đầu đoạn mạch \[AB\] điện áp \[{\user2{u}_3}\user2{ = 3U}\sqrt 2 \,\user2{cos(150\pi t)(V)}\] thì công suất tiêu thụ cùa đoạn mạch là \[{P_3} = \frac{{81}}{{13}}{P_1},\]và hệ số công suất là \[{k_3}\]. Giá trị\[{k_1}\];\[{k_3}\]gần bằng
Câu hỏi trong đề: (2023) Đề thi thử Vật Lí THPT Trần Cao Vân có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn: Dùng chuẩn hóa.
|
ω (rad/s) |
ZL (chuẩn hóa) |
ZC |
Công suất: \[P = \frac{{{U^2}.R}}{{{R^2} + {{({Z_L} - {Z_C})}^2}}}\] |
Hệ số công suất: \[\user2{cos\varphi = }\frac{\user2{R}}{{\sqrt {{\user2{R}^\user2{2}}\user2{ + (}{\user2{Z}_L}\user2{ - Z}_C^{}{\user2{)}^2}} }}\] |
|
50π |
1 |
x |
\[{P_1} = \frac{{{U^2}.R}}{{{R^2} + {{(1 - x)}^2}}}.\] |
\[\user2{cos}{\user2{\varphi }_1}\user2{ = }\frac{\user2{R}}{{\sqrt {{\user2{R}^\user2{2}}\user2{ + (1 - x}{\user2{)}^2}} }}\] |
|
100π |
2 |
x/2 |
\[{P_2} = \frac{{{{(2U)}^2}.R}}{{{R^2} + {{(2 - \frac{x}{2})}^2}}}.\] |
\[\user2{cos}{\user2{\varphi }_2}\user2{ = }\frac{\user2{R}}{{\sqrt {{\user2{R}^\user2{2}}\user2{ + (2 - x/2}{\user2{)}^2}} }}\] |
|
150π |
3 |
x/3 |
\[{P_3} = \frac{{{{(3U)}^2}.R}}{{{R^2} + {{(3 - \frac{x}{3})}^2}}}.\] |
\[\user2{cos}{\user2{\varphi }_3}\user2{ = }\frac{\user2{R}}{{\sqrt {{\user2{R}^\user2{2}}\user2{ + (3 - x/3}{\user2{)}^2}} }}\] |
Khi: ω =50π rad/s: \[{P_1} = \frac{{{U^2}.R}}{{{R^2} + {{({Z_{L1}} - {Z_{C1}})}^2}}} = \frac{{{U^2}.R}}{{{R^2} + {{(1 - x)}^2}}}\];
Khi: ω =100π rad/s: \[{P_2} = \frac{{{{(2U)}^2}.R}}{{{R^2} + {{({Z_{L2}} - {Z_{C2}})}^2}}} = \frac{{{{(2U)}^2}.R}}{{{R^2} + {{(2 - \frac{x}{2})}^2}}} = 4{P_1} = 4\frac{{{U^2}.R}}{{{R^2} + {{(1 - x)}^2}}}.\]
=> \[\begin{array}{l}{(1 - x)^2} = {(2 - \frac{x}{2})^2} \Leftrightarrow 1 - 2{\rm{x}} + {x^2} = 4 - 2{\rm{x + }}\frac{{{x^2}}}{4} = > \frac{{3{x^2}}}{4} = 3 = > x = 2.\\\end{array}\]
Khi: ω =150π rad/s: \[{P_3} = \frac{{{{(3U)}^2}.R}}{{{R^2} + {{({Z_{L3}} - {Z_{C3}})}^2}}} = \frac{{{{(3U)}^2}.R}}{{{R^2} + {{(3 - \frac{x}{3})}^2}}} = \frac{{81}}{{13}}{P_1} = \frac{{81}}{{13}}.\frac{{{U^2}.R}}{{{R^2} + {{(1 - x)}^2}}}.\]
\[\begin{array}{l}13{R^2} + 13{(1 - x)^2} = 9({R^2} + {(3 - \frac{x}{3})^2}) \Rightarrow 4{R^2} + 13 - 26{\rm{x}} + 13{x^2} = 81 - 18{\rm{x + }}{x^2}\\ \Leftrightarrow 4{R^2} = - 12{x^2} + 8x + 68 = > {R^2} = - 3{x^2} + 2x + 17\\x = 2 = > R = 3\end{array}\]
\[{\user2{k}_\user2{1}}\user2{ = cos}{\user2{\varphi }_1}\user2{ = }\frac{\user2{R}}{{\sqrt {{\user2{R}^\user2{2}}\user2{ + (1 - x}{\user2{)}^2}} }}\user2{ = }\frac{3}{{\sqrt {{3^\user2{2}}\user2{ + (1 - 2}{\user2{)}^\user2{2}}} }}\user2{ = }\frac{3}{{\sqrt {10} }}\user2{ = 0,94886}\user2{.}\]
\[{\user2{k}_3}\user2{ = cos}{\user2{\varphi }_3}\user2{ = }\frac{\user2{R}}{{\sqrt {{\user2{R}^\user2{2}}\user2{ + (3 - x/3}{\user2{)}^2}} }}\user2{ = }\frac{3}{{\sqrt {{3^\user2{2}}\user2{ + (3 - 2/3}{\user2{)}^\user2{2}}} }}\user2{ = 0,78935}\user2{.}\] Chọn B.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi A là biên độ bụng, ta có : \[\begin{array}{l}\omega \sqrt {{A^2} - {u^2}} = \frac{{15\pi }}{{100}}v \Leftrightarrow \frac{{2\pi }}{T}\sqrt {{A^2} - {u^2}} = \frac{{15\pi }}{{100}}\frac{\lambda }{T}\\ \Rightarrow \sqrt {{A^2} - {u^2}} = \frac{{15\lambda }}{{200}} = \frac{{15.60}}{{200}} = 4,5cm.\end{array}\]
\[ = > A = \sqrt {4,{5^2} + {6^2}} = 7,5cm\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Giáo dục và Đào tạo Nam Định có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
Đề thi thử tốt nghiệp THPT môn Vật lí Nguyễn Khuyến Lê Thánh Tông - TPHCM có đáp án
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Yên Lạc - Vĩnh Phúc - Lần 1 có đáp án
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Chuyên Phan Bội Châu- Nghệ An - lần 1 có đáp án
Nhắn tin Zalo