Câu hỏi:
18/04/2023 2,291
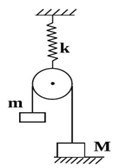
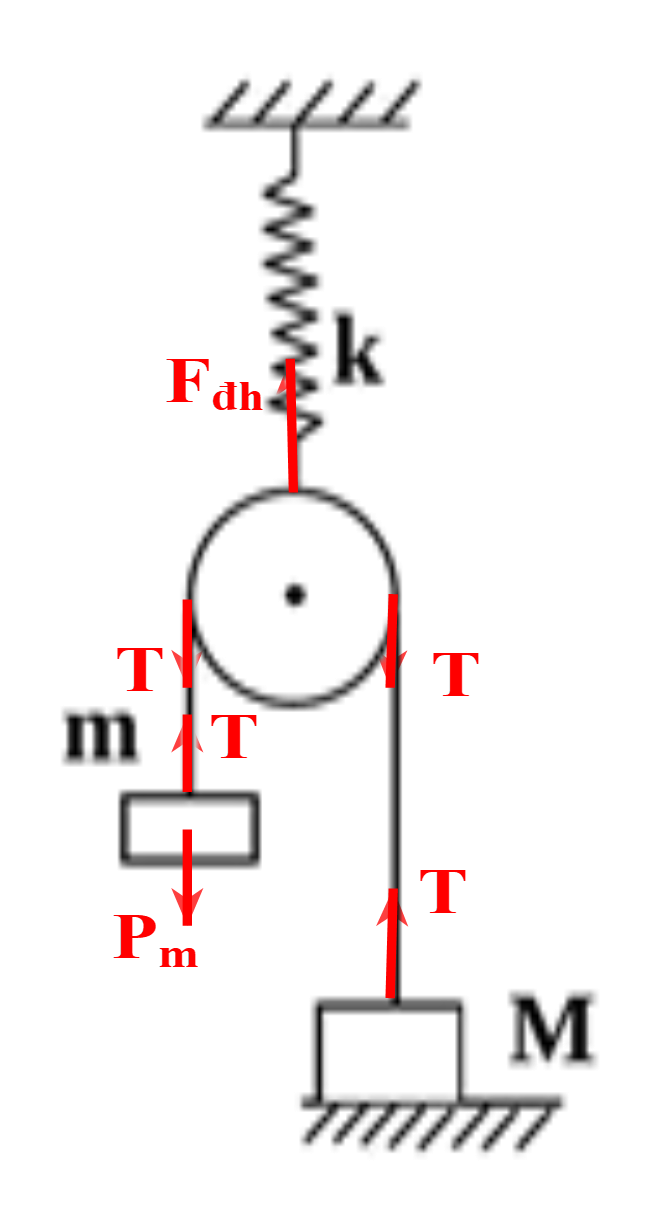
Cho cơ hệ gồm có một vật nặng có khối lượng \(m = 300{\rm{\;g}}\) được buộc vào sợi dây không dãn vắt qua ròng rọc, một đầu dây buộc cố định vào vật khối lượng \({\rm{M}} = 1,2{\rm{\;kg}}\). Ròng rọc được treo vào một lò xo có độ cứng \({\rm{k}} = 150{\rm{\;N}}/{\rm{m}}\). Bỏ qua khối lượng của lò xo, ròng rọc và của dây nối. Tại vị trí cân bằng người ta truyền cho m một vận tốc ban đầu \({{\rm{v}}_0}\) dọc theo trục sợi dây hướng xuống. Lấy \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Tìm giá trị lớn nhất của \({{\rm{v}}_0}\) để \({\rm{m}}\) dao động điều hoà.
Câu hỏi trong đề: (2023) Đề thi thử Vật Lí Đô Lương 1, Nghệ An có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn
Chọn chiều dương hướng xuống
Xét tại vị trí cân bằng \(\left\{ \begin{array}{l}2T - k\Delta {l_0} = 0\\mg - T = 0\end{array} \right. \Rightarrow 2mg - k\Delta {l_0} = 0\)
Xét tại vị trí vật có li độ x thì \(\left\{ \begin{array}{l}2T' - k\left( {\Delta {l_0} + \frac{x}{2}} \right) = 0\\mg - T' = - m{\omega ^2}x\end{array} \right.\)
\( \Rightarrow \left( {2mg - k\Delta {l_0}} \right) + 2m{\omega ^2}x - k.\frac{x}{2} = 0 \Rightarrow \omega = \sqrt {\frac{k}{{4m}}} = \sqrt {\frac{{150}}{{4.0,3}}} = 5\sqrt 5 \) (rad/s)
\(T' = mg + m{\omega ^2}x \Rightarrow T{'_{\max }} = mg + m{\omega ^2}A \le Mg \Rightarrow 0,3.10 + 0,3.{\left( {5\sqrt 5 } \right)^2}A \le 1,2.10 \Rightarrow A \le 0,24m = 24cm\)
\({v_0} = \omega A \le 5\sqrt 5 .24 = 120\sqrt 5 \) (cm/s). Chọn C
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn
\(\tan \left| {{\varphi _{AM}}} \right| = \frac{{{Z_C}}}{R} \Rightarrow \tan \frac{\pi }{4} = \frac{{{Z_C}}}{R} \Rightarrow {Z_C} = R\)
\(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R} \Rightarrow \tan \frac{\pi }{4} = \frac{{{Z_L} - {Z_C}}}{{{Z_C}}} \Rightarrow \frac{{{Z_C}}}{{{Z_L}}} = 0,5\). Chọn A
Lời giải
Hướng dẫn
Chọn C
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Giáo dục và Đào tạo Nam Định có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Trưng Yên - Hưng Yên có đáp án
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Yên Lạc - Vĩnh Phúc - Lần 1 có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 6)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận