Câu hỏi:
12/07/2024 565
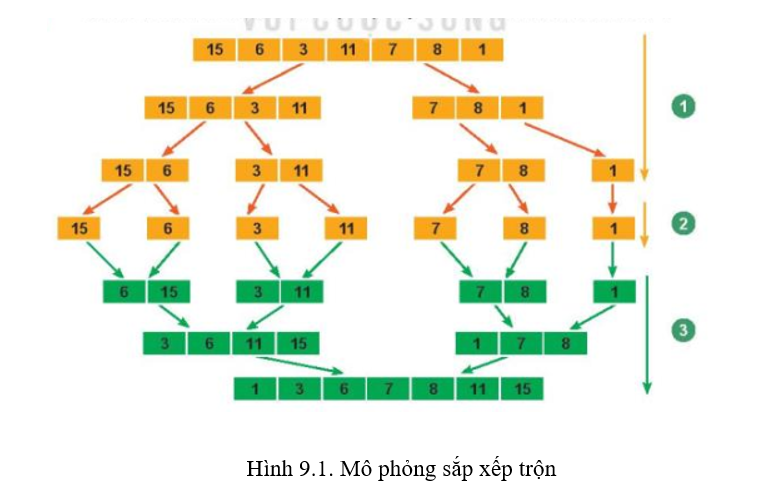
Ta đã biết tìm kiếm nhị phân trên các dãy đã sắp xếp có độ phức tạp thời gian tốt hơn so với các thuật toán tìm kiếm trên dãy chưa sắp xếp. Chính vì thế, việc sắp xếp thông tin theo một trình tự nào đó luôn đóng vai trò quan trọng trong các bài toán tìm kiếm thông tin. Tuy nhiên, một số thuật toán sắp xếp mà em đã biết như sắp xếp chèn, sắp xếp chọn, sắp xếp nổi bọt, ... đều có độ phức tạp thời gian O () (n - kích thước dãy cần sắp xếp). Câu hỏi đặt ra là: Liệu có hay không một cách sắp xếp dãy với thời gian tốt hơn O ()?
Liệu kĩ thuật chia để trị có thể áp dụng cho bài toán sắp xếp được không? Nếu có thì có làm tăng hiệu quả của sắp xếp được không?
Ta đã biết tìm kiếm nhị phân trên các dãy đã sắp xếp có độ phức tạp thời gian tốt hơn so với các thuật toán tìm kiếm trên dãy chưa sắp xếp. Chính vì thế, việc sắp xếp thông tin theo một trình tự nào đó luôn đóng vai trò quan trọng trong các bài toán tìm kiếm thông tin. Tuy nhiên, một số thuật toán sắp xếp mà em đã biết như sắp xếp chèn, sắp xếp chọn, sắp xếp nổi bọt, ... đều có độ phức tạp thời gian O () (n - kích thước dãy cần sắp xếp). Câu hỏi đặt ra là: Liệu có hay không một cách sắp xếp dãy với thời gian tốt hơn O ()?
Liệu kĩ thuật chia để trị có thể áp dụng cho bài toán sắp xếp được không? Nếu có thì có làm tăng hiệu quả của sắp xếp được không?
Câu hỏi trong đề: Chuyên đề Tin Học 11 KNTT Bài 9. Sắp xếp trộn có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Kỹ thuật chia để trị có thể được áp dụng cho bài toán sắp xếp, và thực tế nó đã được sử dụng để thiết kế các thuật toán sắp xếp hiệu quả như QuickSort và MergeSort.
Tuy nhiên, trong thực tế, cách tiếp cận này không phải lúc nào cũng làm tăng hiệu quả của thuật toán sắp xếp. QuickSort và MergeSort, mặc dù sử dụng phương pháp chia để trị, thường là những thuật toán có hiệu quả cao. Nhưng nếu áp dụng phương pháp chia để trị cho một thuật toán sắp xếp khác như BubbleSort hoặc InsertionSort, chẳng hạn, thì không có nhiều lợi ích. Trong những trường hợp đó, việc sử dụng phương pháp chia để trị có thể làm giảm hiệu quả của thuật toán sắp xếp.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đây là một ví dụ về cách viết chương trình bằng ngôn ngữ Python để trộn hai dãy số được lưu trữ trong tệp văn bản "Data.inp" và ghi kết quả vào tệp "Data.out":
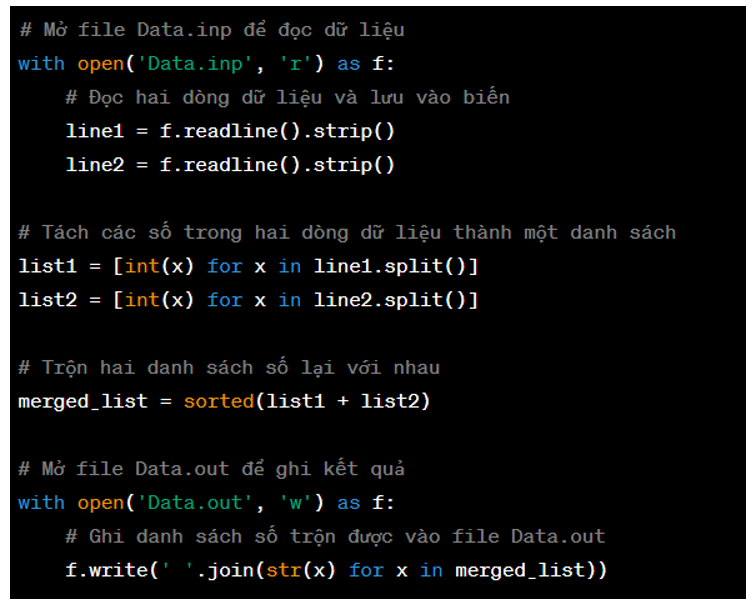
- Đầu tiên, chương trình sử dụng hàm open() để mở tệp "Data.inp" với chế độ đọc dữ liệu (‘r’).
- Sau đó, chương trình đọc hai dòng dữ liệu từ tệp bằng cách sử dụng phương thức readline(), và loại bỏ các ký tự trắng ở đầu và cuối dòng bằng phương thức strip().
- Tiếp theo, chương trình sử dụng phương thức split() để tách các số trong hai dòng dữ liệu thành một danh sách các số nguyên. Hàm int() được sử dụng để chuyển đổi các chuỗi số sang kiểu số nguyên.
- Sau đó, chương trình trộn hai danh sách số lại với nhau bằng cách sử dụng phương thức sorted() để sắp xếp danh sách theo thứ tự tăng dần.
- Cuối cùng, chương trình sử dụng hàm open() để mở tệp "Data.out" với chế độ ghi dữ liệu ('w'), và sử dụng phương thức write() để ghi danh sách số trộn được vào tệp. Hàm join() được sử dụng để chuyển đổi các số trong danh sách trở lại thành chuỗi, và ký tự dấu cách được sử dụng để ngăn cách giữa các số.
Lời giải
1. Đầu tiên, ta cần import các thư viện time và random để thực hiện đo thời gian và sinh số ngẫu nhiên cho dãy số:
2. Tiếp theo, ta sẽ tạo một hàm để sắp xếp dãy số bằng thuật toán sắp xếp nổi bọt
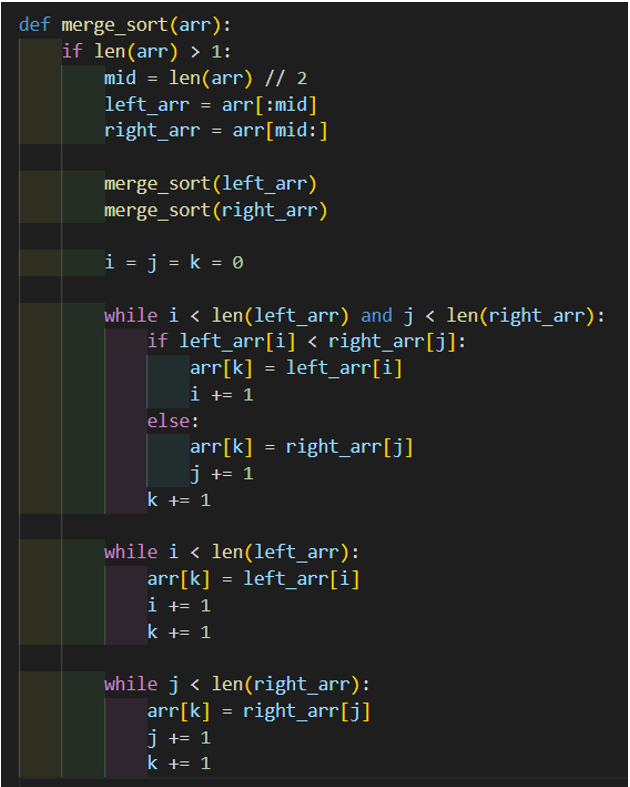
3. Sau đó, ta cần tạo một hàm để sắp xếp dãy số bằng thuật toán sắp xếp trộn:
4. Tiếp theo, ta sẽ đọc dãy số từ tệp văn bản và lưu vào một list:
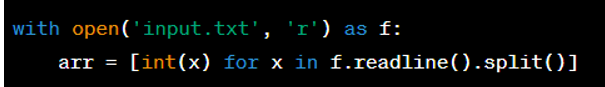
5. Tiếp theo, ta tạo một bản sao của list này để thực hiện sắp xếp bằng hai cách khác nhauz;
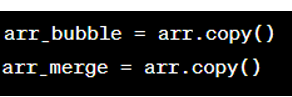
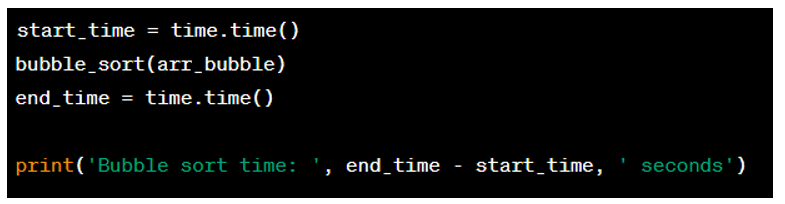
6. Sau đó, ta thực hiện sắp xếp bằng thuật toán sắp xếp nổi bọt và đo thời gian chạy:
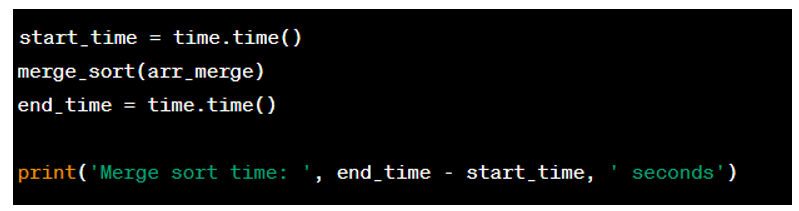
7. Tiếp theo, ta thực hiện sắp xếp bằng thuật toán sắp xếp trộn và đo thời gian chạy:
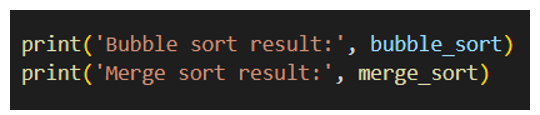
8. In kết quả mảng sau khi sắp xếp:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 4 đề thi cuối học kì 2 Tin 11 Kết nối tri thức có đáp án (Đề 2)
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 26 có đáp án
-
Bộ 4 đề thi cuối học kì 2 Tin 11 Kết nối tri thức có đáp án (Đề 1)
-
15 câu Trắc nghiệm Tin học 11 Cánh diều Bài 1: Một số thao tác chỉnh sửa ảnh và hỗ trợ chỉnh sửa ảnh có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 25 có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 28 có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 27 có đáp án
-
15 câu Trắc nghiệm Tin học 11 Cánh diều Bài 2: Tẩy xóa ảnh có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận