Câu hỏi:
12/07/2024 227
Cùng thực hiện, trao đổi, thảo luận thiết kế chương trình sinh tất cả các dãy nhị phân độ dài n bằng kĩ thuật quay lui.
Cùng thực hiện, trao đổi, thảo luận thiết kế chương trình sinh tất cả các dãy nhị phân độ dài n bằng kĩ thuật quay lui.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Để thiết kế chương trình sinh tất cả các dãy nhị phân độ dài n bằng kĩ thuật quay lui, ta có thể sử dụng đệ quy để thêm lần lượt các số 0 và 1 vào dãy nhị phân.
Bước 1: Viết hàm để sinh dãy nhị phân độ dài n:
Bước 2: Gọi hàm generate_binary_sequence với độ dài của dãy nhị phân cần sinh:
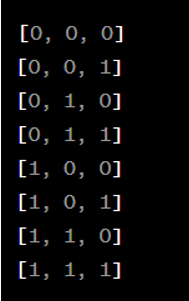
Thu được kết quả:
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
- Lệnh A.pop() tại dòng 8 của chương trình 2 nhằm xóa phần tử đã nhập từ bước trước khi quay lui
- Vì ở chương trình 1, dãy A được thiết lập từ trước có đủ n phần tử nên tại bước này chỉ là lệnh gán giá trị và không cần dùng lệnh pop()
- Ở Chương trình 2, dãy A ban đầu là dãy rộng, do đó A được bổ sung dần. Sau khi kết thúc lệnh gọi đệ quy ở dòng 7 cần gọi lệnh pop() ở dòng 8.
Lời giải
Ý tưởng của thuật toán duyệt quay lui là luôn tìm cách đi tiếp theo. Xuất phát từ vị trí gốc, thuật toán sẽ gọi hàm tìm bước đi tiếp theo. Nếu thực hiện được một bước đi thì gọi lại hàm để tìm bước đi tiếp theo. Nếu không tìm thấy đường đi thì cần "quay lui" về vị trí trước đó để tìm đường đi khác. Thuật toán sẽ sử dụng kĩ thuật đệ quy khi gọi hàm cho bước đi tiếp theo.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 4 đề thi cuối học kì 2 Tin 11 Kết nối tri thức có đáp án (Đề 2)
-
15 câu Trắc nghiệm Tin học 11 Cánh diều Bài 1: Một số thao tác chỉnh sửa ảnh và hỗ trợ chỉnh sửa ảnh có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 25 có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 27 có đáp án
-
15 câu Trắc nghiệm Tin học 11 Cánh diều Bài 2: Tẩy xóa ảnh có đáp án
-
15 câu Trắc nghiệm Tin học 11 Cánh diều Bài 4: Giới thiệu phần mềm làm video có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 24 có đáp án
-
15 câu Trắc nghiệm Tin học 11 Kết nối tri thức Bài 18 có đáp án