Câu hỏi:
14/06/2023 1,320
Cho nửa đường tròn tâm O đường kính AB. Gọi C là 1 điểm nằm trên nửa đường tròn (O) (C khác A và B). Gọi H là hình chiếu vuông góc của C trên AB, D là điểm đối xứng của A qua C, I là trung điểm của CH, J là trung điểm của DH.
a) Chứng minh \[\widehat {CIJ} = \widehat {CBH}\].
b) Chứng minh DCJH ᔕ DHIB.
c) Gọi E là giao điểm của HD và BI. Chứng minh HE.HD = HC2.
Cho nửa đường tròn tâm O đường kính AB. Gọi C là 1 điểm nằm trên nửa đường tròn (O) (C khác A và B). Gọi H là hình chiếu vuông góc của C trên AB, D là điểm đối xứng của A qua C, I là trung điểm của CH, J là trung điểm của DH.
a) Chứng minh \[\widehat {CIJ} = \widehat {CBH}\].
b) Chứng minh DCJH ᔕ DHIB.
c) Gọi E là giao điểm của HD và BI. Chứng minh HE.HD = HC2.
Câu hỏi trong đề:
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
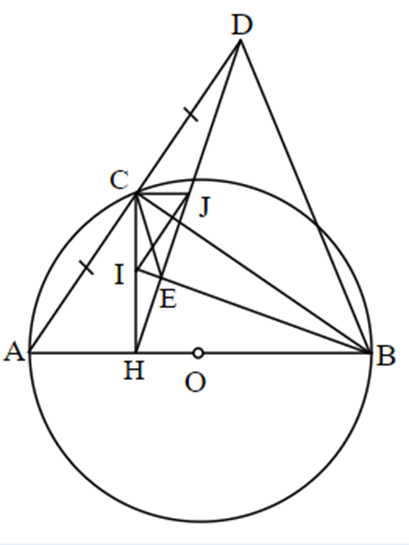
a) Ta có: \[\widehat {CBH} = \widehat {ACH}\] (cùng phụ \[\widehat {HCB}\]) (1)
Xét DCDH ta có:
I và J lần lượt là trung điểm của CH và DH
Þ IJ là đường trung bình của DCHD
Þ IJ // CD Þ IJ // AC Þ \[\widehat {CIJ} = \widehat {ACH}\] (so le trong) (2)
Từ (1) và (2) Þ \[\widehat {CIJ} = \widehat {CBH}\] (đpcm)
b) Thấy CJ là đường trung bình của DADH Þ \[\frac{{CJ}}{{AH}} = \frac{1}{2}\]
Mà \[\frac{{HI}}{{CH}} = \frac{1}{2}\] (Do I là trung điểm của CH) Þ \[\frac{{CJ}}{{AH}} = \frac{{HI}}{{CH}} \Rightarrow \frac{{CJ}}{{HI}} = \frac{{AH}}{{CH}}\]
Dễ chứng minh DAHC ᔕ DCHB \[ \Rightarrow \frac{{AH}}{{CH}} = \frac{{CH}}{{HB}} \Rightarrow \frac{{CJ}}{{HI}} = \frac{{CH}}{{HB}}\]
Lại có: CJ // AB và CH ^ AB Þ CH ^ CJ Þ \[\widehat {JCH} = 90^\circ \]
Xét DCJH và DHIB có:
\[\widehat {JCH} = \widehat {CHB}\]
\[\frac{{CJ}}{{CH}} = \frac{{CH}}{{HB}}\]
Þ DCJH ᔕ DHIB (c. g. c) (đpcm)
c) Ta có: \[\widehat {HIB} + \widehat {HBI} = 90^\circ \].
Mà \[\widehat {HBI} = \widehat {CHJ}\] (do DCJH ᔕ DHIB)
Þ \[\widehat {HIB} + \widehat {CHJ} = 90^\circ \]
Þ DHEI vuông tại E Þ \[\widehat {IEJ} = 90^\circ \]
Xét tứ giác CIEJ: \[\widehat {IEJ} = \widehat {ICJ} = 90^\circ \]Þ Tứ giác CIEJ nội tiếp đường tròn
Þ \[\widehat {ECI} = \widehat {{\rm{EJI}}}\] hay \[\widehat {ECH} = \widehat {HJI}\]. Mà \[\widehat {HJI} = \widehat {HDC}\](vì IJ // CD) Þ \[\widehat {ECH} = \widehat {HDC}\]
Xét DHEC và DHCD có:
\[\widehat {ECH} = \widehat {CDH}\] (cmt)
\[\widehat {CHD}\]: chung
Do đó DHEC ᔕ DHCD (g.g)
Suy ra: \[\frac{{HE}}{{HC}} = \frac{{HC}}{{HD}} \Rightarrow HE.HD = H{C^2}\] (đpcm).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hai lớp 5A và 5B tham gia trồng cây. Tuy số học sinh hai lớp bằng nhau nhưng lớp 5B trồng nhiều hơn lớp 5A là 5 cây. Tìm số cây mỗi lớp trồng được, biết nếu mỗi bạn lớp 5A trồng 3 cây thì lớp đó thừa 2 cây, nếu mỗi bạn lớp 5B trồng 4 cây thì lớp đó thiếu 38 cây.
Hai lớp 5A và 5B tham gia trồng cây. Tuy số học sinh hai lớp bằng nhau nhưng lớp 5B trồng nhiều hơn lớp 5A là 5 cây. Tìm số cây mỗi lớp trồng được, biết nếu mỗi bạn lớp 5A trồng 3 cây thì lớp đó thừa 2 cây, nếu mỗi bạn lớp 5B trồng 4 cây thì lớp đó thiếu 38 cây.
Xem đáp án »
12/07/2024
3,705
Câu 2:
Biết rằng cứ 3 thùng mật ong đựng được 27 lít. Trong kho có 12 thùng, ngoài cửa hàng có 5 thùng. Hỏi tất cả có bao nhiêu lít mật ong?
Biết rằng cứ 3 thùng mật ong đựng được 27 lít. Trong kho có 12 thùng, ngoài cửa hàng có 5 thùng. Hỏi tất cả có bao nhiêu lít mật ong?
Xem đáp án »
12/07/2024
3,098
Câu 3:
Một cửa hàng nhập về 3 đợt, trung bình mỗi đợt 150 kg đường. Đợt một nhập 170 kg và nhập ít hơn đợt hai 40 kg. Hỏi đợt ba cửa hàng đã nhập về bao nhiêu kg?
Một cửa hàng nhập về 3 đợt, trung bình mỗi đợt 150 kg đường. Đợt một nhập 170 kg và nhập ít hơn đợt hai 40 kg. Hỏi đợt ba cửa hàng đã nhập về bao nhiêu kg?
Xem đáp án »
12/07/2024
2,652
Câu 4:
Một số chia hết cho 6 và 8. Tìm số đó biết thương khi chia cho 6 lớn hơn thương khi chia cho 8 là 4 đơn vị.
Một số chia hết cho 6 và 8. Tìm số đó biết thương khi chia cho 6 lớn hơn thương khi chia cho 8 là 4 đơn vị.
Xem đáp án »
12/07/2024
2,608
Câu 6:
Tìm số tự nhiên x biết 144 chia hết cho x, 192 chia hết cho x, 240 chia hết cho x và x là số tự nhiên có hai chữ số.
Tìm số tự nhiên x biết 144 chia hết cho x, 192 chia hết cho x, 240 chia hết cho x và x là số tự nhiên có hai chữ số.
Xem đáp án »
12/07/2024
2,155
Câu 7:
Một thửa ruộng hình chữ nhật có chiều dài gấp đôi chiều rộng. Nếu chiều rộng tăng thêm 20 m, chiều dài thêm 15 m thì chiều dài gấp rưỡi chiều rộng. Tính diện tích thửa ruộng đó?
Một thửa ruộng hình chữ nhật có chiều dài gấp đôi chiều rộng. Nếu chiều rộng tăng thêm 20 m, chiều dài thêm 15 m thì chiều dài gấp rưỡi chiều rộng. Tính diện tích thửa ruộng đó?
Xem đáp án »
12/07/2024
2,149
về câu hỏi!