Câu hỏi:
14/06/2023 365
Cho hai đoạn thẳng AB và CD cắt nhau ở E. Các tia phân giác các góc ACE và DBE cắt nhau ở K. Chứng ming rằng: \(\widehat {BKC} = \frac{{\widehat {BAC} + \widehat {BDC}}}{2}\).
Cho hai đoạn thẳng AB và CD cắt nhau ở E. Các tia phân giác các góc ACE và DBE cắt nhau ở K. Chứng ming rằng: \(\widehat {BKC} = \frac{{\widehat {BAC} + \widehat {BDC}}}{2}\).
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
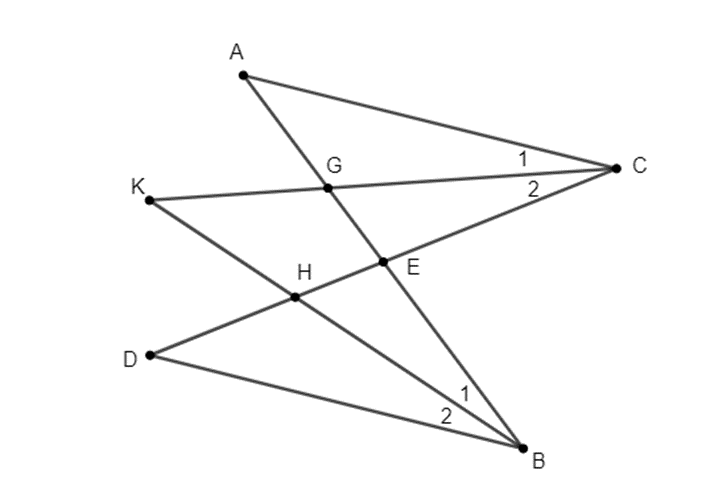
Gọi G là giao điểm của CK và AE, H là giao điểm của BK và DE.
Xét ∆KGB và ∆AGC và theo tính chất góc ngoài của tam giác ta có:
\(\left\{ \begin{array}{l}\widehat K + \widehat {{B_1}} = \widehat {AGK}\\\widehat A + \widehat {{C_1}} = \widehat {AGK}\end{array} \right. \Rightarrow \widehat K + \widehat {{B_1}} = \widehat A + \widehat {{C_1}}\) (1)
Xét ∆KHC và ∆DHB và theo tính chất góc ngoài của tam giác, ta có:
\(\left\{ \begin{array}{l}\widehat K + {\widehat C_2} = \widehat {EHB}\\\widehat D + {\widehat B_2} = \widehat {EHB}\end{array} \right.\)
\( \Rightarrow \widehat K + {\widehat C_2} = \widehat D + {\widehat B_2}\) (2)
Do \({\widehat B_1} = {\widehat B_2}\) (BK là tia phân giác của \(\widehat {DBA}\))
\({\widehat C_1} = {\widehat C_2}\) (CK là tia phân giác của \(\widehat {ACD}\))
Cộng (1) và (2) ta được: \(2\widehat K = \widehat A + \widehat D\).
Do đó \(\widehat K = \frac{{\widehat A + \widehat D}}{2}\).
Vậy \(\widehat {BKC} = \frac{{\widehat {BAC} + \widehat {BDC}}}{2}\)(đpcm)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới)
Đã bán 1,5k
₫ 70.000
₫ 36.000
Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết)
Đã bán 986
₫ 70.000
₫ 36.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hiện nay, mẹ hơn con 24 tuổi. Cách đây 3 năm, tuổi con bằng \(\frac{1}{4}\) tuổi mẹ. Tính tuổi của mỗi người hiện nay.
Hiện nay, mẹ hơn con 24 tuổi. Cách đây 3 năm, tuổi con bằng \(\frac{1}{4}\) tuổi mẹ. Tính tuổi của mỗi người hiện nay.
Xem đáp án »
12/07/2024
8,053
Câu 3:
Một bếp ăn dự trữ gạo đủ cho 120 người ăn trong 50 ngày. Nhưng thực tế đã có một số người đến thêm nên số gạo đó chỉ đủ ăn trong 30 ngày. Hỏi số người đến thêm là bao nhiêu?
Một bếp ăn dự trữ gạo đủ cho 120 người ăn trong 50 ngày. Nhưng thực tế đã có một số người đến thêm nên số gạo đó chỉ đủ ăn trong 30 ngày. Hỏi số người đến thêm là bao nhiêu?
Xem đáp án »
12/07/2024
5,085
Câu 4:
Cho A = 20 + 21 + 22 + 23 + 24 + … + 219 và B = 220. Chứng minh A và B là hai số tự nhiên liên tiếp.
Cho A = 20 + 21 + 22 + 23 + 24 + … + 219 và B = 220. Chứng minh A và B là hai số tự nhiên liên tiếp.
Xem đáp án »
12/07/2024
4,347
Câu 5:
Tìm x:
a) 2016 : [25 – (3x + 2)] = 32.7
b) 6x + x = 511 : 59 + 31
Tìm x:
a) 2016 : [25 – (3x + 2)] = 32.7
b) 6x + x = 511 : 59 + 31
Xem đáp án »
12/07/2024
3,830
Câu 7:
Hai ngăn sách có tất cả 70 quyển. Nếu ngăn trên thêm 6 quyển và ngăn dưới bớt đi 1 quyển thì ngăn dưới hơn ngăn trên 3 quyển. Tính số sách ở mỗi ngăn.
Hai ngăn sách có tất cả 70 quyển. Nếu ngăn trên thêm 6 quyển và ngăn dưới bớt đi 1 quyển thì ngăn dưới hơn ngăn trên 3 quyển. Tính số sách ở mỗi ngăn.
Xem đáp án »
11/07/2024
3,447
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận