Câu hỏi:
13/07/2024 435
Cho đường tròn (O; R). Vẽ hai bán kính OA, OB. Trên các bán kính OA, OB lần lượt lấy các điểm M, N sao cho OM = ON. Vẽ dây CD đi qua M, N (M nằm giữa C và N).
a) Chứng minh CM = DN.
Cho đường tròn (O; R). Vẽ hai bán kính OA, OB. Trên các bán kính OA, OB lần lượt lấy các điểm M, N sao cho OM = ON. Vẽ dây CD đi qua M, N (M nằm giữa C và N).
a) Chứng minh CM = DN.
Quảng cáo
Trả lời:
Giải bởi Vietjack
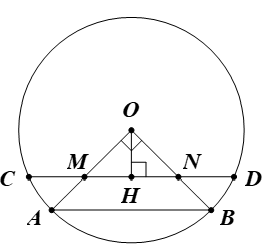
a) Kẻ OH ⊥ CD (H ∈ CD).
Suy ra H là trung điểm CD.
Do đó HC = HD (quan hệ giữa đường kính và dây cung) (1)
Tam giác OMN cân tại O (do OM = ON).
Suy ra OH vừa là đường cao, vừa là đường trung tuyến của tam giác OMN.
Do đó HM = HN (2)
Lại có CH = CM + MH và DH = DN + NH (3)
Từ (1), (2), (3), suy ra CM = DN.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có:
⦁ Thứ năm đầu tiên là ngày 2.
⦁ Thứ năm thứ hai là ngày 9.
⦁ Thứ năm thứ ba là ngày 16.
⦁ Thứ năm thứ tư là ngày 23.
⦁ Thứ năm thứ năm là ngày 30.
Ta không thể chọn thứ năm đầu tiên là ngày 1 hoặc ngày 3 vì trong tháng đó có 3 ngày thứ 5 trùng vào ngày chẵn.
Vậy ngày 26 của tháng đó là ngày Chủ nhật.
Lời giải
Tóm tắt: 750 người: 40 ngày.
? người: 25 ngày.
Bài giải
Số người ăn hết số gạo trong 1 ngày là:
750 . 40 = 30 000 (người).
Số người ăn hết gạo đơn vị đã chuẩn bị trong 25 ngày là:
30 000 : 25 = 1 200 (người).
Số người chuyển đến thêm là:
1 200 – 750 = 450 (người).
Đáp số: 450 người.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận