Câu hỏi:
12/07/2024 689
Cho tam giác nhọn ABC. Các đường cao AD và BE cắt nhau tại H. Đường thẳng vuông góc với AB tại A cắt BE ở K. Chứng minh tam giác EAK đồng dạng tam giác ECH.
Cho tam giác nhọn ABC. Các đường cao AD và BE cắt nhau tại H. Đường thẳng vuông góc với AB tại A cắt BE ở K. Chứng minh tam giác EAK đồng dạng tam giác ECH.
Câu hỏi trong đề:
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
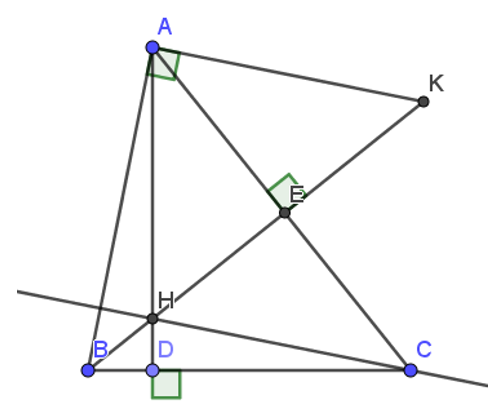
Vì H là giao của 2 đường cao AD, BE trong tam giác nên H là trực tâm.
Do đó, CH cũng là đường cao của tam giác ABC hay CH vuông góc với AB
Mà AK vuông góc với AB (giả thiết)
Suy ra: CH song song với AK
(so le trong)
Xét tam giác EAK và ECH có:
Do đó, tam giác EAK đồng dạng với tam giác ECH (g.g).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
. Người ta muốn chia 374 quyển vở, 68 thước kẻ va 340 nhãn vở thành một số phần thưởng như nhau. Hỏi có thể chia được nhiều nhất bao nhiêu phần thưởng, mỗi phần thưởng có bao nhiêu quyển vở, thước kẻ, nhãn vở ?
. Người ta muốn chia 374 quyển vở, 68 thước kẻ va 340 nhãn vở thành một số phần thưởng như nhau. Hỏi có thể chia được nhiều nhất bao nhiêu phần thưởng, mỗi phần thưởng có bao nhiêu quyển vở, thước kẻ, nhãn vở ?
Xem đáp án »
12/07/2024
11,354
Câu 2:
Có bao nhiêu số nguyên là tổng của ba phần tử phân biệt của tập hợp {1; 4; 7; 10; 13; 16; 19}.
Có bao nhiêu số nguyên là tổng của ba phần tử phân biệt của tập hợp {1; 4; 7; 10; 13; 16; 19}.
Xem đáp án »
12/07/2024
6,209
Câu 4:
Một đội công nhân có 8 người làm trong 6 ngày đắp được 360m đường. Hỏi một đội công nhân có 12 người đắp xong 1080m đường trong bao nhiêu ngày ?
Một đội công nhân có 8 người làm trong 6 ngày đắp được 360m đường. Hỏi một đội công nhân có 12 người đắp xong 1080m đường trong bao nhiêu ngày ?
Xem đáp án »
12/07/2024
4,407
Câu 5:
Tìm hai số có tổng là 234, biết rằng nếu lấy số thứ nhất trừ đi số thứ hai rồi cộng với hiệu của chúng thì được 172.
Tìm hai số có tổng là 234, biết rằng nếu lấy số thứ nhất trừ đi số thứ hai rồi cộng với hiệu của chúng thì được 172.
Xem đáp án »
12/07/2024
3,646
Câu 6:
Một đồng hồ treo tường có đặc điểm như sau: Khi kim phút chỉ đúng số 12 thì đồng hồ đánh số chuông tương ứng với số mà kim giờ chỉ. Hỏi một ngày đồng hồ phải đánh bao nhiêu tiếng chuông ?
Một đồng hồ treo tường có đặc điểm như sau: Khi kim phút chỉ đúng số 12 thì đồng hồ đánh số chuông tương ứng với số mà kim giờ chỉ. Hỏi một ngày đồng hồ phải đánh bao nhiêu tiếng chuông ?
Xem đáp án »
12/07/2024
3,565
Câu 7:
Tìm hai số có tổng là 132. Biết rằng nếu lấy số lớn trừ đi số bé rồi cộng vó tổng của chúng thì được 178.
Tìm hai số có tổng là 132. Biết rằng nếu lấy số lớn trừ đi số bé rồi cộng vó tổng của chúng thì được 178.
Xem đáp án »
12/07/2024
3,557
về câu hỏi!