Câu hỏi:
27/06/2023 1,902
Cho hai nguồn sóng kết hợp \({{\rm{S}}_1}{{\rm{S}}_2}\) trên mặt chất lỏng cách nhau 15 cm, dao động với phương trình là \({{\rm{u}}_{{{\rm{S}}_1}}} = {{\rm{u}}_{{{\rm{S}}_2}}} = 2{\rm{cos}}10{\rm{\pi t\;}}\left( {{\rm{cm}}} \right)\) (t tính bằng giây). Tốc độ truyền sóng trên mặt chất lỏng là \(10{\rm{\;cm}}/{\rm{s}}\). Coi biên độ dao động không đổi khi truyền đi. Điểm \({\rm{M}}\) nằm trên đường thẳng vuông góc với \({{\rm{S}}_1}{{\rm{S}}_2}\) tại \({{\rm{S}}_2}\) cách \({{\rm{S}}_1}\) là \(25{\rm{\;cm}}\). Khoảng cách giữa hai điểm gần \({{\rm{S}}_2}\) nhất và xa \({{\rm{S}}_2}\) nhất có tốc độ dao động cực đại bằng \(20{\rm{\pi }}\sqrt 2 {\rm{\;}}\left( {{\rm{cm}}/{\rm{s}}} \right)\) trên đoạn \({{\rm{S}}_2}{\rm{M}}\) là
Cho hai nguồn sóng kết hợp \({{\rm{S}}_1}{{\rm{S}}_2}\) trên mặt chất lỏng cách nhau 15 cm, dao động với phương trình là \({{\rm{u}}_{{{\rm{S}}_1}}} = {{\rm{u}}_{{{\rm{S}}_2}}} = 2{\rm{cos}}10{\rm{\pi t\;}}\left( {{\rm{cm}}} \right)\) (t tính bằng giây). Tốc độ truyền sóng trên mặt chất lỏng là \(10{\rm{\;cm}}/{\rm{s}}\). Coi biên độ dao động không đổi khi truyền đi. Điểm \({\rm{M}}\) nằm trên đường thẳng vuông góc với \({{\rm{S}}_1}{{\rm{S}}_2}\) tại \({{\rm{S}}_2}\) cách \({{\rm{S}}_1}\) là \(25{\rm{\;cm}}\). Khoảng cách giữa hai điểm gần \({{\rm{S}}_2}\) nhất và xa \({{\rm{S}}_2}\) nhất có tốc độ dao động cực đại bằng \(20{\rm{\pi }}\sqrt 2 {\rm{\;}}\left( {{\rm{cm}}/{\rm{s}}} \right)\) trên đoạn \({{\rm{S}}_2}{\rm{M}}\) là
Câu hỏi trong đề: (2023) Đề thi thử Vật Lí Sở GD Yên Bái có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
\(\lambda = v.\frac{{2\pi }}{\omega } = 10.\frac{{2\pi }}{{10\pi }} = 2cm\)
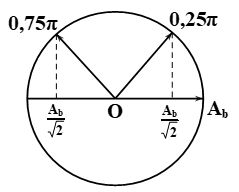
\(A = \frac{{{v_{\max }}}}{\omega } = \frac{{20\pi \sqrt 2 }}{{10\pi }} = 2\sqrt 2 cm = \frac{{{A_b}}}{{\sqrt 2 }}\)
\( \Rightarrow \)pha biên độ lệch \(0,25\pi \) hoặc \(0,75\pi \) \( \Rightarrow \)bậc có dạng ,25 hoặc ,75
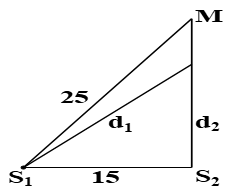
\(\frac{{M{S_1} - M{S_2}}}{\lambda } < k < \frac{{{S_1}{S_2}}}{\lambda } \Rightarrow \frac{{25 - \sqrt {{{25}^2} - {{15}^2}} }}{2} < k < \frac{{15}}{2} \Rightarrow 2,5 < k < 7,5\)
\({d_1} - {d_2} = k\lambda \Rightarrow \sqrt {d_2^2 + {{15}^2}} - {d_2} = k.2 \Rightarrow \left\{ \begin{array}{l}k = 2,75 \Rightarrow {d_2} \approx 17,7cm\\k = 7,25 \Rightarrow {d_2} \approx 0,5cm\end{array} \right.\)
\(\Delta {d_2} = 17,7 - 0,5 = 17,2cm\). Chọn A
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\(\omega = 2\pi f = 2\pi .2 = 4\pi \) (rad/s)
\(A = \sqrt {{x^2} + {{\left( {\frac{v}{\omega }} \right)}^2}} = \sqrt {{5^2} + {{\left( {\frac{{20\pi }}{{4\pi }}} \right)}^2}} = 5\sqrt 2 \) (cm)
\(x = 5cm = \frac{A}{{\sqrt 2 }} \downarrow \Rightarrow \varphi = \frac{\pi }{4}\). Chọn D
Lời giải
\({Z_C} = \frac{1}{{\omega C}} = \frac{T}{{2\pi C}}\), Chọn C
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Giáo dục và Đào tạo Nam Định có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
Đề thi thử tốt nghiệp THPT môn Vật lí Nguyễn Khuyến Lê Thánh Tông - TPHCM có đáp án
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Yên Lạc - Vĩnh Phúc - Lần 1 có đáp án
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Chuyên Phan Bội Châu- Nghệ An - lần 1 có đáp án