Cho hình thang ABCD có AB // CD (AB < CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với hai đáy của hình thang cắt hai đường chéo BD và AC tại E và F, cắt BC tại N. Chứng minh rằng N, E, F lần lượt là trung điểm của BC, BD, AC.
Cho hình thang ABCD có AB // CD (AB < CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với hai đáy của hình thang cắt hai đường chéo BD và AC tại E và F, cắt BC tại N. Chứng minh rằng N, E, F lần lượt là trung điểm của BC, BD, AC.
Quảng cáo
Trả lời:
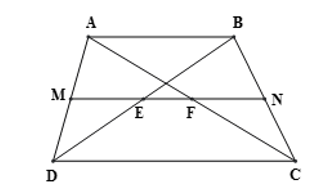
Xét hình thang ABCD có:
MA = MD
N ∈ BC
MN // AB // CD
Suy ra N là trung điểm của BC.
Xét có:
MA = MD; MF // DC
⇒ FA = FC ⇒ F là trung điểm của AC.
Xét có:
MA = MD; ME // AB
⇒ DE = BE ⇒ E là trung điểm của BDHot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Kí hiệu A và B lần lượt là tập các học sinh học giỏi môn hóa và môn văn.
Ta có A ∪ B = 40. Theo quy tắc cộng mở rộng ta có:
n (A ∩ B) = n(A) + n(B) − n(A ∪ B) = 30 + 25 – 40 = 15
Vậy có 15 em học giỏi cả 2 môn.
Lời giải
Diện tích của một viên gạch lát nền là:
40 × 40 = 1600 (cm2)
Diện tích căn phòng là:
1600 × 200 = 320000 (cm2) = 32 m2
Đáp số: 32 m2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.