Trong toán học, n giai thừa (kí hiệu n!) là tích của n số nguyên dương đầu tiên n!=n x (n-1) x …x 1. Vậy ta có thể dùng công thức sau đây để tính n! được không?
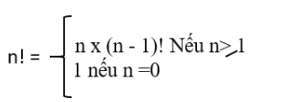
Trong toán học, n giai thừa (kí hiệu n!) là tích của n số nguyên dương đầu tiên n!=n x (n-1) x …x 1. Vậy ta có thể dùng công thức sau đây để tính n! được không?
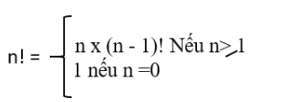
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có thể dùng công thức trên để tính m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Để xây dựng phân đệ quy cho h(n), em hãy xác định lời giải của bài toán khi có 0 người trong phòng từ lời giải của bài toán khi có n - 1 người trong phòng.
a) Trước hết ta nhận thấy rằng nếu có 2 người A và B bắt tay nhau tức là A đã bắt tay B và ngược lại B cũng bắt tay A.
Vì có 10 người nên mỗi người sẽ bắt tay với 10 – 1 = 9 người còn lại.
Tổng số lượt bắt tay của tất cả 10 người là: 10 x 9 = 90.
Do A bắt tay B thì B cũng bắt tay A nên số lần bắt tay ở trên đã được tính 2 lần.
=> Có 90 : 2 = 45 cái bắt tay.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Công thức 2 mang tính đệ quy
Sử dụng công thức ( 2 ) để tiếp tục quá trình tính toán, ta có F{n -1)- F(n - 2)+ F(n - 3), f( n - 2) = F(n - 3) + F(n - 4)... Do đó, nếu cứ gọi đến hàm F như vậy thÌ việc tính toán sẽ không có điểm dừng nên ta phải bỎ sang trường hợp đặc biệt được tính toán sẵn là hàm F tại n = 0 có giá trị 0 và tại n - 1 có giá trị 1. Công thức ( 2) là công thức mang tính đệ quy.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập