Câu hỏi:
03/07/2023 4,884
Một hộp đựng 7 viên bi xanh, 5 viên bi đỏ và 4 viên bi vàng. Có bao nhiêu cách lấy ra 8 viên bi có đủ 3 màu?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Đáp án đúng là: A
Số cách lấy ra 8 viên bi bất kì: \(C_{16}^8 = 12\,\,870\)
Số cách lấy ra 8 viên bi không có màu vàng mà chỉ có hai màu xanh và đỏ: \(C_7^7C_5^1 + C_7^6C_5^2 + C_7^5C_5^3 + C_7^4C_5^4 + C_7^3C_5^5 = 495\)
Số cách lấy ra 8 viên bi không có màu đỏ mà có hai màu xanh và vàng:
\(C_7^7C_4^1 + C_7^6C_4^2 + C_7^5C_4^3 + C_7^4C_4^4 = 165\)
Số cách lấy ra 8 viên bi không có màu xanh mà chỉ có hai màu đỏ và vàng:
\(C_5^5C_4^3 + C_5^4C_4^4 = 9\)
Số cách lấy ra 8 viên bi có đủ 3 màu:
12 870 − (495 + 165 + 9) = 12 201 (cách).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
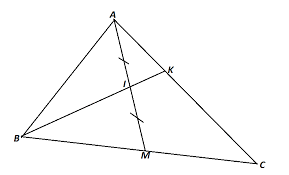
Ta có: \[\left\{ \begin{array}{l}\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {AI} \\\overrightarrow {BI} = \overrightarrow {BM} + \overrightarrow {MI} \end{array} \right.\]
\[ \Rightarrow 2\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {BM} + \left( {\overrightarrow {AI} + \overrightarrow {MI} } \right) = \overrightarrow {BA} + \overrightarrow {BM} = \overrightarrow {BA} + \frac{{\overrightarrow {BC} }}{2}\]
\[ \Rightarrow 4\overrightarrow {BI} = 2\overrightarrow {BA} + \overrightarrow {BC} \]
Lại có: \(\overrightarrow {BK} = \overrightarrow {BA} + \overrightarrow {AK} = \overrightarrow {BA} + \frac{{\overrightarrow {AC} }}{3}\)
\( \Rightarrow 3\overrightarrow {BK} = 3\overrightarrow {BA} + \overrightarrow {AC} = 2\overrightarrow {BA} + \overrightarrow {BC} \)
Do đó: \(4\overrightarrow {BI} = 3\overrightarrow {BK} \) ⇒ B, I, K thẳng hàng.
Lời giải
Lời giải
Gọi A là biến cố “ba viên bi lấy được chỉ có hai màu”
Ta có: Số phần tử của không gian mẫu: \(C_{16}^3 = 560\)
Số cách chọn được ba viên bi chỉ có một màu: \(C_4^3 + C_5^3 + C_7^3 = 49\)
Số cách chọn được ba viên bi có đủ ba màu: \(C_4^1 + C_5^1 + C_7^1 = 140\)
Vậy xác suất cần tìm là: \({\rm P}\left( A \right) = 1 - \frac{{49 + 140}}{{560}} = \frac{{53}}{{80}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận