Trong những câu sau đây, câu nào đúng khi nói về kĩ thuật quay lui?
a) Kĩ thuật quay lui không thể, liệt kê tất cả các trường hợp có thể xảy ra để tìm được nghiệm của bài toán.
b) Khi cài đặt kĩ thuật quay lui, bắt buộc phải sử dụng kĩ thuật đệ quy.
c) Kĩ thuật quay lui là một kĩ thuật theo ý tưởng của kĩ thuật duyệt.
Trong những câu sau đây, câu nào đúng khi nói về kĩ thuật quay lui?
a) Kĩ thuật quay lui không thể, liệt kê tất cả các trường hợp có thể xảy ra để tìm được nghiệm của bài toán.
b) Khi cài đặt kĩ thuật quay lui, bắt buộc phải sử dụng kĩ thuật đệ quy.
c) Kĩ thuật quay lui là một kĩ thuật theo ý tưởng của kĩ thuật duyệt.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trong những câu sau đây, câu sau đúng khi nói về kĩ thuật quay lui:
a) Kĩ thuật quay lui không thể, liệt kê tất cả các trường hợp có thể xảy ra để tìm được nghiệm của bài toán.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
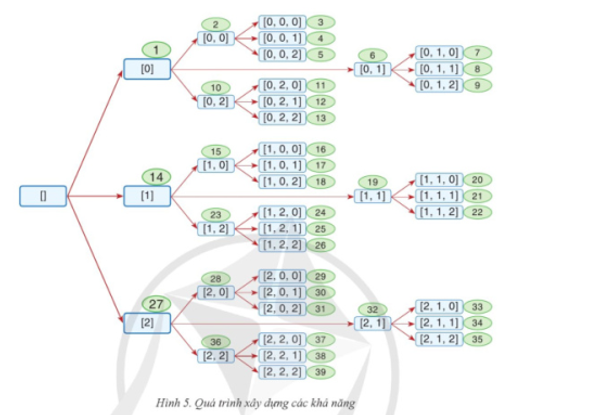
Dãy bit độ dài n có dạng X = (x0,x1...xn-1), trong đó x1 bằng 0 hoặc 1 (0 <i<n-1) có thể mô tả theo cách đệ quy như sau:
- Nếu n > 0 thì phần tử đầu tiên của dãy bằng 0 hoặc 1 và n - 1 phần tử sau là dãy bit độ dài n - 1
- Ngược lại, nếu n = 0 thì dãy bit độ dài n là dãy rỗng
Việc xây dựng các dãy nhị phân theo thuật toán đệ quy như sau:
1. Bắt đầu từ X rỗng, lệnh x = [] và gọi thủ tục đệ quy backtrack(0) để xây dựng bắt đầu phần tử 0.
2. Thành phần i (0<i<n-1) sẽ lần lượt nhận giá trị 0 và 1 bằng lệnh for v in range(2): Với mỗi giá trị của v, thành phần i được ghi nhận vào xi của X bằng lệnh x.append(v). lệnh này đây v vào cuối ÀV Sau đó tiếp tục gợi để quy để xây dựng các thành phần còn lại (từ thành phần Xi+1... đến thành phần x.)
3. Để xét được khả năng tiếp theo, hành động quay lui được thực hiện bằng cách loại bỏ nhị phân thành phần cuối cùng của X bằng lệnh x.pop(). Việc quay lui cũng được diễn ra khí đang xây dựng thành phần x mà x, đã lần lượt nhận cả hai giá trị 0 và 1, khi đó thành phân x sẽ bị loại khỏi X và lùi về để xét khả năng tiếp theo cho thành phần Xi-1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
n = int(input("Nhap n:"))
if ( n<2 or n % 2 == 0or n % 3 == 0 or n % 5 == 0):
print("không phải số nguyên tố ")
else:print("là số nguyên tố")
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập