Câu hỏi:
12/07/2024 224
Cho (O; R) và (O; R’) tiếp xúc ngoài tại A. Kẻ dây cung AM của (O) và dây cung AN của (O’) sao cho AM vuông góc với AN chứng minh:
a) OM // O’N.
b) Xác định vị trí của AM và AN để diện tích tứ giác OMNO’ lớn nhất.
Cho (O; R) và (O; R’) tiếp xúc ngoài tại A. Kẻ dây cung AM của (O) và dây cung AN của (O’) sao cho AM vuông góc với AN chứng minh:
a) OM // O’N.
b) Xác định vị trí của AM và AN để diện tích tứ giác OMNO’ lớn nhất.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
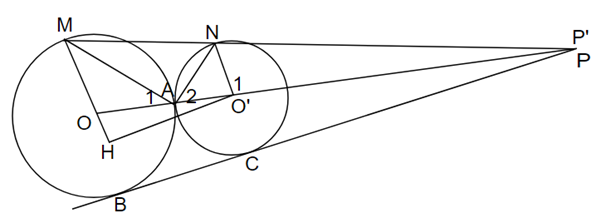
a) Ta có : \(\widehat {MOA} = {\widehat O_1}\left( { = {{180}^{\rm{o}}} - 2{{\widehat A}_1}} \right)\)
Þ O’N // OM.
Gọi P là giao điểm của MN và OO’.
Ta có : \(\frac{{O'P}}{{OP}} = \frac{{O'N}}{{OM}} = \frac{{R'}}{R}\)
Gọi P’ là giao điểm của BC và OO’, ta có:
\(\frac{{O'P'}}{{OP'}} = \frac{{O'C}}{{OB}} = \frac{{R'}}{R}\)
Suy ra P’ ≡ P.
b) Gọi H là hình chiếu của O' trên OM
Tứ giác MNO'O là hình thang nên \(S = \frac{{\left( {OM + O'N} \right)O'H}}{2}\)
\(S = \frac{{R + R'}}{2} \cdot O'H \le \frac{{R + R'}}{2}.OO' = \frac{{{{\left( {R + R'} \right)}^2}}}{2}\)
Dấu "=" xảy ra khi \(H \equiv O \Leftrightarrow OM \bot OO'\)
Vậy để diện tích tứ giác OMNO’ lớn nhất thì OM ⊥ OO’.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới)
Đã bán 1,5k
₫ 70.000
₫ 36.000
Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết)
Đã bán 986
₫ 70.000
₫ 36.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hai tập hợp A = {x ∈ ℝ | 1≤ |x| ≤ 2}; B = (–∞; m – 2] ∪ [m; +∞).
Tìm tất cả các giá trị của m để A ⊂ B.
Cho hai tập hợp A = {x ∈ ℝ | 1≤ |x| ≤ 2}; B = (–∞; m – 2] ∪ [m; +∞).
Tìm tất cả các giá trị của m để A ⊂ B.
Xem đáp án »
13/07/2024
38,951
Câu 2:
Cho tập hợp A = (0; +∞) và B = {x ∈ ℝ | mx2 ‒ 4x + m ‒ 3 = 0}. Tìm m để B có đúng hai tập con và B ⊂ A.
Cho tập hợp A = (0; +∞) và B = {x ∈ ℝ | mx2 ‒ 4x + m ‒ 3 = 0}. Tìm m để B có đúng hai tập con và B ⊂ A.
Xem đáp án »
05/04/2025
23,423
Câu 3:
Từ các số 1, 2, 3, 4, 5 có thể lập được bao nhiêu số có 3 chữ số khác nhau chia hết cho 3.
Từ các số 1, 2, 3, 4, 5 có thể lập được bao nhiêu số có 3 chữ số khác nhau chia hết cho 3.
Xem đáp án »
13/07/2024
15,842
Câu 4:
Lớp 10A có 45 học sinh, trong đó 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Sử, 6 em không thích môn nào trong 3 môn trên và 5 em thích cả 3 môn. Hỏi có bao nhiêu em thích 1 môn trong 3 môn trên?
Lớp 10A có 45 học sinh, trong đó 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Sử, 6 em không thích môn nào trong 3 môn trên và 5 em thích cả 3 môn. Hỏi có bao nhiêu em thích 1 môn trong 3 môn trên?
Xem đáp án »
13/07/2024
13,246
Câu 5:
Cho các tập hợp \(A = \left[ {1 - m;\frac{{m + 3}}{2}} \right]\) và B = (‒∞; ‒3) ∪ [3; +∞). Tìm tất cả các số thực m để A ∪ B = ℝ.
Cho các tập hợp \(A = \left[ {1 - m;\frac{{m + 3}}{2}} \right]\) và B = (‒∞; ‒3) ∪ [3; +∞). Tìm tất cả các số thực m để A ∪ B = ℝ.
Xem đáp án »
13/07/2024
8,811
Câu 6:
Cho hàm số \[y = f\left( x \right) = \frac{{3x + 1}}{{1 - x}}\] (C). Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành.
Cho hàm số \[y = f\left( x \right) = \frac{{3x + 1}}{{1 - x}}\] (C). Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành.
Xem đáp án »
13/07/2024
6,192
Câu 7:
Tứ giác có hai góc đối bằng 90° có phải là hình chữ nhật không?
Tứ giác có hai góc đối bằng 90° có phải là hình chữ nhật không?
Xem đáp án »
13/07/2024
3,153
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận