Câu hỏi:
13/07/2024 2,720
Cho tam giác ABC vuông cân tại A, \[AB = \sqrt 2 \]. Về phía ngoài tam giác vẽ tam giác ACD vuông cân tại D .
a) Tứ giác ABCD là hình gì? Vì sao?
b) Tính diện tích ABCD.
Cho tam giác ABC vuông cân tại A, \[AB = \sqrt 2 \]. Về phía ngoài tam giác vẽ tam giác ACD vuông cân tại D .
a) Tứ giác ABCD là hình gì? Vì sao?
b) Tính diện tích ABCD.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
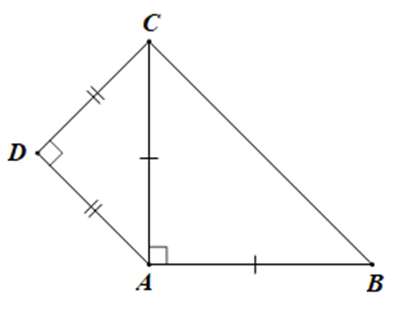
∆ABC vuông cân \[ \Rightarrow \widehat {ABC} = \widehat {ACB}\].
∆ADC vuông cân tại D \[ \Rightarrow \widehat {ACD} = \widehat {DAC}\].
Ta có: \[\widehat {BCD} = \widehat {ACB} + \widehat {ACD} = {45^{\rm{o}}} + {45^{\rm{o}}} = {90^{\rm{o}}}\]
⇒ BC ⊥ CD
Ta lại có AD ⊥ CD ⇒ AD // BC
Xét tứ giác ADCB có:
AD // BC, \[\widehat {ADC} = \widehat {DCB} = {90^{\rm{o}}}\].
⇒ ADCB là hình thang vuông
Khi đó \[BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {2 + 2} = 2\]
Xét ∆ADC vuông cân tại D có: \[\sin \widehat {DCA} = \frac{{AD}}{{AC}}\]
\[ \Rightarrow AD = \sin \widehat {DCA}.AC = \sin {45^{\rm{o}}}.\sqrt 2 = \frac{{\sqrt 2 }}{2}.\sqrt 2 = 1\].
⇒ AD = DC = 1.
Vậy diện tích hình thang vuông ADCB là:
\[S = \frac{{AD + BC}}{2}.CD = \frac{{1 + 2}}{2}.1 = \frac{3}{2}\].
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: \[A = \left[ { - 2; - 1} \right] \cup \left[ {1;2} \right]\]; \[B = \left( { - \infty ;m - 2} \right] \cup \left[ {m; + \infty } \right)\]
Để A ⊂ B, ta có:
TH1: \[\left\{ \begin{array}{l}m - 2 \ge - 1\\m \le 1\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}m \ge 1\\m \le 1\end{array} \right.\]\[ \Leftrightarrow m = 1\].
TH2. m ≤ 2.
TH3. m ‒ 2 ≥ 2 ⇔ m ≥ 4.
Vậy \[\left[ \begin{array}{l}m \ge 4\\m \le - 2\\m = 1\end{array} \right.\] thì A ⊂ B.
Lời giải
Để B có đúng 2 tập con thì B có duy nhất một phần tử, và B ⊂ A nên B có một phần tử thuộc A.
Nên mx2 ‒ 4x + m ‒ 3 = 0 (1) có nghiệm duy nhất và nghiệm đó lớn hơn 0.
Với m = 0, ta có phương trình: (loại).
Với m ≠ 0, phương trình (1) có nghiệm duy nhất lớn hơn 0 khi và chỉ khi:
∆’ = 4 – m(m – 3) = 0.
Với m = –1, ta có: –x2 – 4x – 4 = 0 ⇔ x = –2 (loại).
Với m = 4, ta có: 4x2 – 4x + 1 = 0.
Phương trình có nghiệm .
Vậy m = 4 thỏa yêu cầu bài toán.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận