Một hộ nông dân trồng đậu và cà trên diện tích 8a. Nếu trồng đậu thì cần 20 công và thu 3 000 000 đồng trên một a, nếu trồng cà thì cần 30 công và thu 40 000 000 đồng trên một a. Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180?

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gọi x là diện tích trồng đậu, y là diện tích trồng cà, (đơn vị a = 100 m²), điều kiện $x \ge 0,y \ge 0$, ta có $x + y \le 8$.

Số công cần dùng là $20x + 30y \le 180$ hay $2x + 3y \le 18$.

Số tiền thu được là

$F = 3000000x + 4000000y{\rm{\;}}$(đồng)

Hay $F = 3x + 4y$ (triệu đồng)

Ta cần tìm x, y thỏa mãn hệ bất phương trình $\left\{ {\begin{array}{*{20}{l}}{x + y \le 8}\\{2x + 3y \le 18}\\{x \ge 0}\\{y \ge 0}\end{array}} \right.$

Sao cho $F = 3x + 4y$ đạt giá trị lớn nhất.

Biểu diễn tập nghiệm của $\left( {\rm{H}} \right)$ ta được miền tứ giác ${\rm{OABC}}$ với ${\rm{A}}\left( {0;6} \right),{\rm{B}}\left( {6;2} \right)$, $C\left( {8;0} \right)$ và $O\left( {0;0} \right)$.

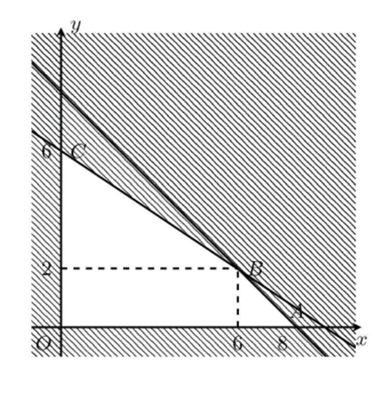
Một hộ nông dân trồng đậu và cà trên diện tích 8a. Nếu trồng đậu thì cần 20 công và (ảnh 1)

Xét giá trị của ${\rm{F}}$ tại các đỉnh ${\rm{O}},{\rm{A}},{\rm{B}},{\rm{C}}$ và so sánh ta suy ra $x = 6,y = 2$ (tọa độ điểm B) là diện tích cần trồng mỗi loại để thu được nhiều tiền nhất là ${\rm{F}} = 26$ (triệu đồng).

Đáp số: Trồng 6 (a) đậu, 2 (a) cà, thu hoạch 26 000 000 đồng.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hai tập hợp A = {x ∈ ℝ | 1≤ |x| ≤ 2}; B = (–∞; m – 2] ∪ [m; +∞).

Tìm tất cả các giá trị của m để A ⊂ B.

Xem đáp án

Lời giải

Ta có: \[A = \left[ { - 2; - 1} \right] \cup \left[ {1;2} \right]\]; \[B = \left( { - \infty ;m - 2} \right] \cup \left[ {m; + \infty } \right)\]

Để A ⊂ B, ta có:

TH1: \[\left\{ \begin{array}{l}m - 2 \ge - 1\\m \le 1\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}m \ge 1\\m \le 1\end{array} \right.\]\[ \Leftrightarrow m = 1\].

TH2. m ≤ 2.

TH3. m ‒ 2 ≥ 2 ⇔ m ≥ 4.

Vậy \[\left[ \begin{array}{l}m \ge 4\\m \le - 2\\m = 1\end{array} \right.\] thì A ⊂ B.

Câu 2

Cho tập hợp A = (0; +∞) và B = {x ∈ ℝ | mx² ‒ 4x + m ‒ 3 = 0}. Tìm m để B có đúng hai tập con và B ⊂ A.

Xem đáp án

Lời giải

$- 4 x - 3 = 0 \Leftrightarrow x = \frac{- 3}{4}$

Để B có đúng 2 tập con thì B có duy nhất một phần tử, và B ⊂ A nên B có một phần tử thuộc A.

Nên mx² ‒ 4x + m ‒ 3 = 0 (1) có nghiệm duy nhất và nghiệm đó lớn hơn 0.

Với m = 0, ta có phương trình: (loại).

Với m ≠ 0, phương trình (1) có nghiệm duy nhất lớn hơn 0 khi và chỉ khi:

∆’ = 4 – m(m – 3) = 0.

$\Leftrightarrow - m^{2} + 3 m + 4 = 0 \Leftrightarrow [\begin{array}{l} m = - 1 \\ m = 4 \end{array}$

Với m = –1, ta có: –x² – 4x – 4 = 0 ⇔ x = –2 (loại).

Với m = 4, ta có: 4x² – 4x + 1 = 0.

Phương trình có nghiệm $x = \frac{1}{2} > 0$ .

Vậy m = 4 thỏa yêu cầu bài toán.

Câu 3