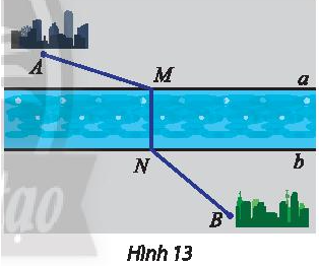
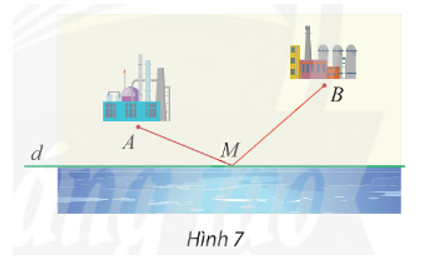
Trong các hình sau, hình nào có trục đối xứng?
Có phép biến hình nào biến một nửa mỗi hình phẳng sau đây thành nửa còn lại không?

Trong các hình sau, hình nào có trục đối xứng?
Có phép biến hình nào biến một nửa mỗi hình phẳng sau đây thành nửa còn lại không?

Quảng cáo
Trả lời:
⦁ Trong các hình đã cho, cả ba hình đều có trục đối xứng là đường thẳng màu vàng ở mỗi hình.
⦁ Ta xét hình chiếc lá:
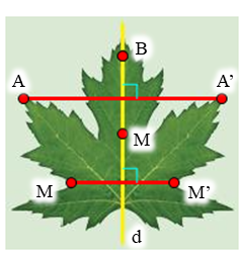
Lấy điểm A bất kì trên chiếc lá sao cho A không nằm trên trục đối xứng d của chiếc lá (hình vẽ).
Khi đó ta luôn xác định được một điểm A’ đối xứng với A qua d hay d là đường trung trực của đoạn thẳng AA’.
Tương tự như vậy, với mỗi điểm M bất kì trên chiếc lá sao cho M không nằm trên d, ta đều xác định được một điểm M’ sao cho d là đường trung trực của đoạn thẳng MM’ (1)
Lấy điểm B bất kì trên chiếc lá sao cho B nằm trên đường thẳng d (hình vẽ).
Khi đó ta có B đối xứng với chính nó qua d.
Tương tự như vậy, với mỗi điểm M bất kì trên chiếc lá sao cho M nằm trên d thì ta luôn có M đối xứng với chính nó qua d (2)
Từ (1), (2), ta thu được phép biến hình biến một nửa chiếc lá thành nửa còn lại là phép biến hình biến mỗi điểm M không thuộc trục đối xứng d thành điểm M’ sao cho d là đường trung trực của đoạn MM’ và biến mỗi điểm M thuộc d thành chính nó.
Chứng minh tương tự với hình cây thông và hình con bọ, ta cũng được kết quả như trên.
Vậy phép biến hình cần tìm là phép biến hình biến mỗi điểm M không thuộc trục đối xứng d của mỗi hình phẳng thành điểm M’ sao cho d là đường trung trực của đoạn MM’ và biến mỗi điểm M thuộc d thành chính nó.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Trục Oy: x = 0.
Thế x = 0 vào phương trình d, ta được 0 – y + 3 = 0 ⇔ y = 3.
Suy ra giao điểm của d và Oy là P(0; 3).
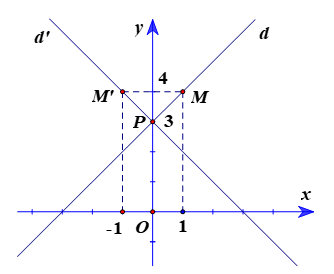
Chọn điểm M(1; 4) ∈ d: x – y + 3 = 0
Ta đặt M’ = ĐOy(M).
Suy ra Oy là đường trung trực của MM’ hay M’ là điểm đối xứng với M qua Oy.
Do đó hai điểm M và M’ có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ điểm M’(–1; 4).
Ta có .
Gọi d’ là ảnh của d qua ĐOy.
Đường thẳng d’ có vectơ chỉ phương .
Suy ra d’ có vectơ pháp tuyến .
Vậy đường thẳng d’ đi qua P(0; 3) và có vectơ pháp tuyến nên phương trình d’ là: 1.(x – 0) + 1.(y – 3) = 0 hay x + y – 3 = 0.
b) Đường tròn (C) có tâm I(–1; –2), bán kính R = 3.
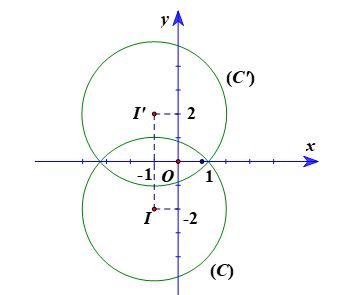
Ta đặt I’ = ĐOx(I).
Suy ra Ox là đường trung trực của II’ hay I’ đối xứng với I qua Ox
Do đó hai điểm I và I’ có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ điểm I’(–1; 2).
Gọi (C’) là ảnh của đường tròn (C) qua ĐOx.
Suy ra (C’) có tâm I’(–1; 2), bán kính R’ = R = 3.
Vậy phương trình đường tròn (C’): (x + 1)2 + (y – 2)2 = 9.
Lời giải
Đường tròn (C) có tâm I(3; 4), bán kính R = 5.
a)
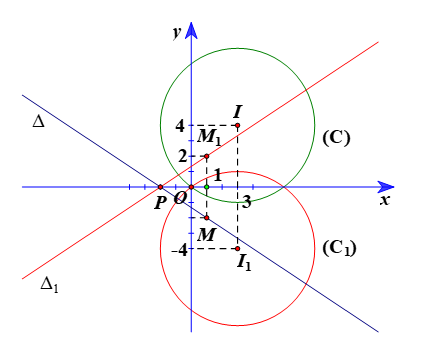
⦁ Gọi (C1) là ảnh của (C) qua ĐOx, khi đó (C1) có tâm I1 là ảnh của I(3; 4) ĐOx và bán kính R1 = R = 5.
Ta có I1 = ĐOx(I).
Suy ra Ox là đường trung trực của đoạn II1
Do đó hai điểm I(3; 4) và I1 có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ I1(3; –4).
Vậy ảnh của đường tròn (C) qua ĐOx là đường tròn (C1) có phương trình là:
(x – 3)2 + (y + 4)2 = 25.
⦁ Trục Ox: y = 0.
Với y = 0, ta có 2x + 3.0 + 4 = 0 ⇔ x = –2.
Suy ra giao điểm của ∆ và trục Ox là điểm P(–2; 0).
Khi đó P = ĐOx(P).
Chọn M(1; –2) ∈ ∆.
Gọi M1 và ∆1 theo thứ tự là ảnh của M và ∆ qua ĐOx.
Ta thấy Ox là đường trung trực của đoạn MM1.
Do đó hai điểm M(1; –2) và M1 có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ M1(1; 2).
Ta có .
Đường thẳng ∆1 có vectơ chỉ phương .
Suy ra ∆1 có vectơ pháp tuyến .
Vậy đường thẳng ∆1 đi qua P(–2; 0) và có vectơ pháp tuyến nên có phương trình là:
2(x + 2) – 3(y – 0) = 0 hay 2x – 3y + 4 = 0.
b)
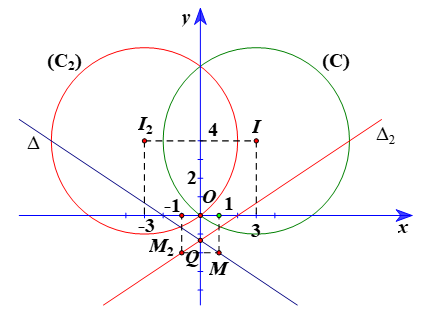
⦁ Gọi (C2) là ảnh của (C) qua ĐOy, khi đó (C2) có tâm I2 là ảnh của I(3; 4) qua ĐOy và bán kính R2 = R = 5.
Ta có I2 = ĐOy(I).
Suy ra Oy là đường trung trực của đoạn II2.
Do đó hai điểm I(3; 4) và I2 có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ I2(–3; 4).
Vậy ảnh của đường tròn (C) qua ĐOy là đường tròn (C2) có phương trình là:
(x + 3)2 + (y – 4)2 = 25.
⦁ Trục Oy: x = 0.
Với x = 0, ta có 2.0 + 3y + 4 = 0 ⇔ .
Suy ra giao điểm của ∆ và trục Oy là điểm .
Khi đó Q = ĐOy(Q).
Chọn M(1; –2) ∈ ∆.
Gọi M2 và ∆2 theo thứ tự là ảnh của M và ∆ qua ĐOy.
Ta thấy Oy là đường trung trực của đoạn MM2.
Do đó hai điểm M(1; –2) và M2 có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ M2(–1; –2).
Ta có .
Đường thẳng ∆2 có vectơ chỉ phương .
Suy ra ∆2 có vectơ pháp tuyến .
Vậy đường thẳng ∆2 đi qua M2(–1; –2) và có vectơ pháp tuyến nên có phương trình là:
2(x + 1) – 3(y + 2) = 0 hay 2x – 3y – 4 = 0.
c)
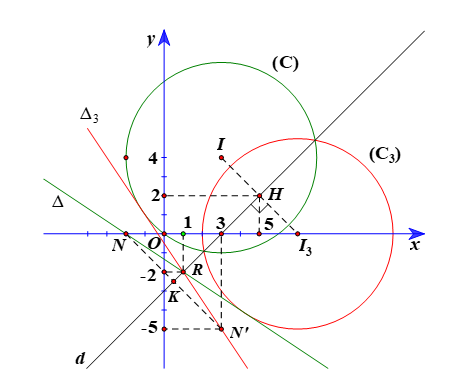
⦁ Gọi (C3) là ảnh của (C) qua Đd, khi đó (C2) có tâm I3 là ảnh của I(3; 4) qua Đd và bán kính R3 = R = 5.
Ta có I3 = Đd(I).
Suy ra d là đường trung trực của đoạn II3 nên II3 ⊥ d tại trung điểm của II3.
Mà đường thẳng d: x – y – 3 = 0 có vectơ pháp tuyến .
Suy ra đường thẳng II3 có vectơ chỉ phương .
Do đó đường thẳng II3 có vectơ pháp tuyến .
Vì vậy đường thẳng II3 đi qua điểm I(3; 4) và nhận làm vectơ pháp tuyến nên có phương trình là:
1(x – 3) + 1(y – 4) = 0 ⇔ x + y – 7 = 0.
Gọi H là giao điểm của II3 và đường thẳng d.
Suy ra tọa độ H thỏa mãn hệ phương trình
Do đó tọa độ H(5; 2).
Ta có H là trung điểm II3.
Suy ra
Do đó tọa độ I3(7; 0).
Vậy ảnh của đường tròn (C) qua Đd là đường tròn (C3) có phương trình là:
(x – 7)2 + y2 = 25.
⦁ Gọi R là giao điểm của ∆ và d.
Suy ra tọa độ R thỏa mãn hệ phương trình:
Do đó tọa độ R(1; –2).
Khi đó R = Đd(R).
Chọn N(–2; 0) ∈ ∆: 2x + 3y + 4 = 0.
Gọi N’ và ∆3 theo thứ tự là ảnh của N và ∆ qua Đd.
Ta thấy d là đường trung trực của đoạn NN’.
Mà đường thẳng d: x – y – 3 = 0 có vectơ pháp tuyến .
Suy ra đường thẳng NN’ có vectơ chỉ phương .
Do đó đường thẳng NN’ có vectơ pháp tuyến .
Vì vậy đường thẳng NN’ đi qua N(–2; 0) và nhận làm vectơ pháp tuyến nên có phương trình là:
1(x + 2) + 1(y – 0) = 0 ⇔ x + y + 2 = 0.
Gọi K là giao điểm của NN’ và đường thẳng d.
Suy ra tọa độ K thỏa mãn hệ phương trình:
Do đó tọa độ .
Ta có K là trung điểm NN’.
Suy ra
Do đó tọa độ N’(3; –5).
Với R(1; –2), ta có .
Đường thẳng ∆3 có vectơ chỉ phương .
Suy ra ∆3 có vectơ pháp tuyến .
Vậy đường thẳng ∆3 đi qua N’(3; –5) và nhận làm vectơ pháp tuyến nên có phương trình là:
3(x – 3) + 2(y + 5) = 0 hay 3x + 2y + 1 = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.