Chuyên đề Toán 11 CTST Bài 3. Phép đối xứng trục có đáp án
31 người thi tuần này 4.6 4.5 K lượt thi 15 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
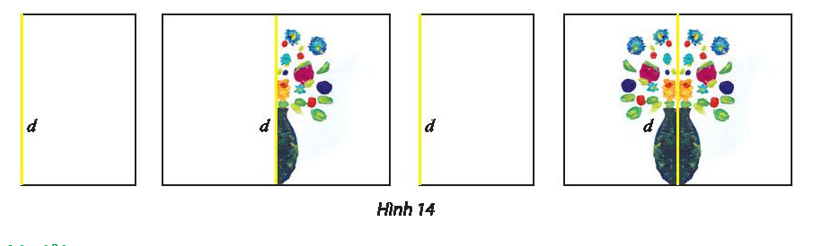
⦁ Trong các hình đã cho, cả ba hình đều có trục đối xứng là đường thẳng màu vàng ở mỗi hình.
⦁ Ta xét hình chiếc lá:
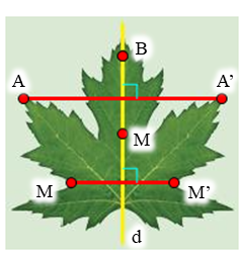
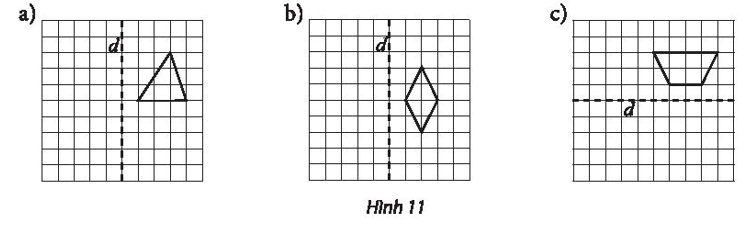
Lấy điểm A bất kì trên chiếc lá sao cho A không nằm trên trục đối xứng d của chiếc lá (hình vẽ).
Khi đó ta luôn xác định được một điểm A’ đối xứng với A qua d hay d là đường trung trực của đoạn thẳng AA’.
Tương tự như vậy, với mỗi điểm M bất kì trên chiếc lá sao cho M không nằm trên d, ta đều xác định được một điểm M’ sao cho d là đường trung trực của đoạn thẳng MM’ (1)
Lấy điểm B bất kì trên chiếc lá sao cho B nằm trên đường thẳng d (hình vẽ).
Khi đó ta có B đối xứng với chính nó qua d.
Tương tự như vậy, với mỗi điểm M bất kì trên chiếc lá sao cho M nằm trên d thì ta luôn có M đối xứng với chính nó qua d (2)
Từ (1), (2), ta thu được phép biến hình biến một nửa chiếc lá thành nửa còn lại là phép biến hình biến mỗi điểm M không thuộc trục đối xứng d thành điểm M’ sao cho d là đường trung trực của đoạn MM’ và biến mỗi điểm M thuộc d thành chính nó.
Chứng minh tương tự với hình cây thông và hình con bọ, ta cũng được kết quả như trên.
Vậy phép biến hình cần tìm là phép biến hình biến mỗi điểm M không thuộc trục đối xứng d của mỗi hình phẳng thành điểm M’ sao cho d là đường trung trực của đoạn MM’ và biến mỗi điểm M thuộc d thành chính nó.
Lời giải
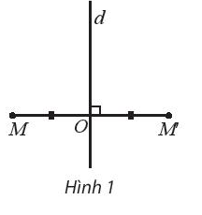
Theo đề, ta có f(M) = M’.
Ta thấy f là quy tắc sao cho ứng với mỗi điểm M, ta đều xác định được duy nhất một điểm M’.
Vậy f là một phép biến hình.
Lời giải
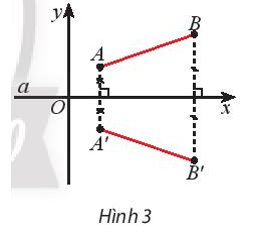
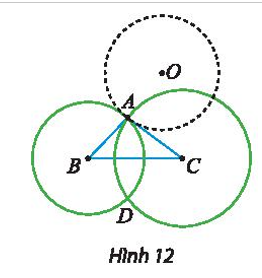
⦁ Ta có A’ là ảnh của A qua Đa.
Suy ra a là đường trung trực của đoạn thẳng AA’ hay Ox là đường trung trực của đoạn thẳng AA’.
Do đó A’ đối xứng với A qua Ox nên chúng có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ A’(xA; –yA).
Tương tự như vậy, ta được tọa độ B’(xB; –yB).
Vậy tọa độ A’(xA; –yA) và B’(xB; –yB).
⦁ Ta có .
Suy ra .
Ta lại có .
Suy ra .
Vậy A’B’ = AB.
Lời giải
a) Trục Oy: x = 0.
Thế x = 0 vào phương trình d, ta được 0 – y + 3 = 0 ⇔ y = 3.
Suy ra giao điểm của d và Oy là P(0; 3).
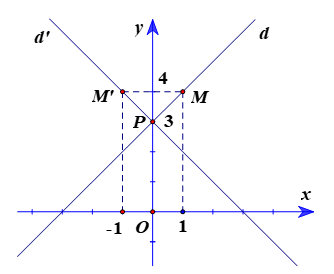
Chọn điểm M(1; 4) ∈ d: x – y + 3 = 0
Ta đặt M’ = ĐOy(M).
Suy ra Oy là đường trung trực của MM’ hay M’ là điểm đối xứng với M qua Oy.
Do đó hai điểm M và M’ có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ điểm M’(–1; 4).
Ta có .
Gọi d’ là ảnh của d qua ĐOy.
Đường thẳng d’ có vectơ chỉ phương .
Suy ra d’ có vectơ pháp tuyến .
Vậy đường thẳng d’ đi qua P(0; 3) và có vectơ pháp tuyến nên phương trình d’ là: 1.(x – 0) + 1.(y – 3) = 0 hay x + y – 3 = 0.
b) Đường tròn (C) có tâm I(–1; –2), bán kính R = 3.
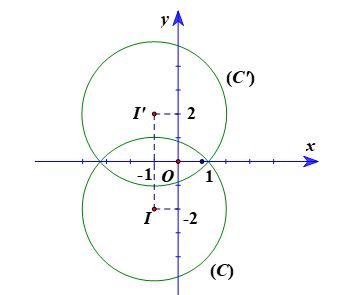
Ta đặt I’ = ĐOx(I).
Suy ra Ox là đường trung trực của II’ hay I’ đối xứng với I qua Ox
Do đó hai điểm I và I’ có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ điểm I’(–1; 2).
Gọi (C’) là ảnh của đường tròn (C) qua ĐOx.
Suy ra (C’) có tâm I’(–1; 2), bán kính R’ = R = 3.
Vậy phương trình đường tròn (C’): (x + 1)2 + (y – 2)2 = 9.
Lời giải
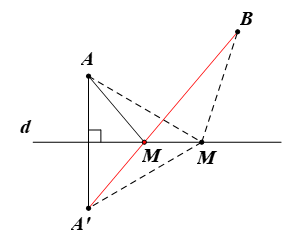
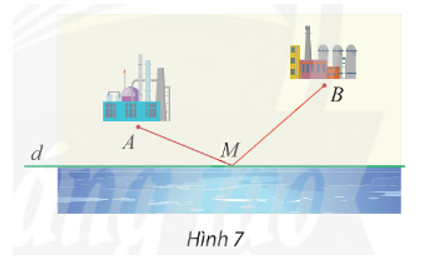
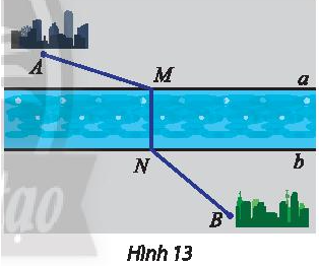
Gọi A’ là ảnh của A qua Đd.
Suy ra d là đường trung trực của đoạn thẳng AA’.
Mà M ∈ d (giả thiết), do đó MA = MA’.
Vì AB cố định nên A’B cũng cố định.
Ta có MA + MB = MA’ + MB ≥ A’B (theo bất đẳng thức tam giác).
Suy ra MA + MB ngắn nhất khi và chỉ khi MA + MB = A’B.
Tức là, ba điểm A’, M, B thẳng hàng hay M là giao điểm của A’B và d.
Vậy địa điểm M cần tìm là giao điểm của bờ sông (đường thẳng d) với đường thẳng A’B, trong đó A’ là ảnh của A qua Đd.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.