Chuyên đề Toán 11 CTST Bài 6. Phép vị tự có đáp án
44 người thi tuần này 4.6 4.5 K lượt thi 17 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
⦁ Những hình như vậy có cùng hình dạng nhưng khác kích thước.
⦁ Ta xét cụ thể một hình là hình hai con mèo:
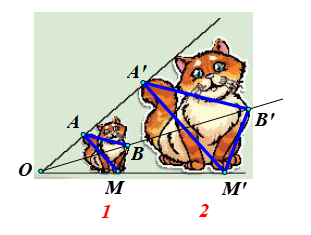
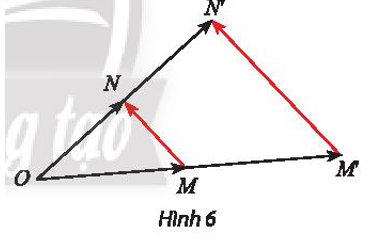
• Giả sử O là điểm cố định trên hình hai con mèo, M là một điểm trên hình con mèo 1 (như hình vẽ).
Lấy điểm M’ là điểm sao cho (k > 0), khi đó điểm M’ có vị trí trên hình con mèo 2 tương ứng với điểm M trên hình con mèo 1.
Lấy điểm A’ sao cho , với k > 0, ta được điểm A’ có vị trí trên hình con mèo 2 tương ứng với điểm A trên hình con mèo 1.
Tương tự như vậy, với mỗi điểm B bất kì trên hình con mèo 1, ta lấy điểm B’ sao cho (k > 0) thì ta được tập hợp các điểm B’ tạo thành hình con mèo 2.
Vì vậy phép biến hình biến hình con mèo 1 thành hình con mèo 2 là phép biến hình biến mỗi điểm N bất kì thành điểm N’ sao cho .
• Chứng minh tương tự với các hình ảnh khác, ta cũng được kết quả như trên.
Vậy phép biến hình cần tìm là phép biến hình biến mỗi điểm M bất kì trên hình kia thành điểm M’ trên hình này sao cho , với O là điểm cố định và k là một số thực, k ≠ 0.
Lời giải
Ta có .
⦁ Gọi M1(x1; y1), ta có .
Theo đề, ta có V(O, 3)(M) = M1.
Suy ra .
Do đó
Vì vậy tọa độ M1(9; 27).
⦁ Gọi M2(x2; y2), ta có .
Theo đề, ta có V(O, –2)(M) = M2.
Suy ra .
Do đó
Vì vậy tọa độ M2(–6; –18).
Vậy M1(9; 27) và M2(–6; –18).
Lời giải
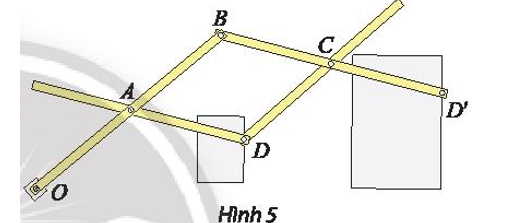
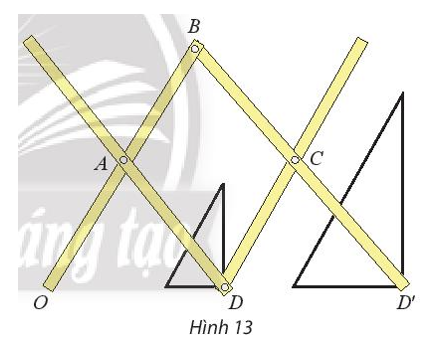
a) Do ba điểm O, D, D’ thẳng hàng (giả thiết), suy ra .
Do đó V(O, k)(D) = D’ và OD’ = |k|.OD.
Vì D, D’ nằm cùng phía đối với O nên k > 0.
Suy ra .
Ta có AB // BD’ (do ABCD là hình bình hành) và ba điểm O, D, D’ thẳng hàng (giả thiết).
Khi đó áp dụng định lí Thales, ta được .
Vậy phép vị tự cần tìm là .
b) Từ câu a, ta có (k > 0).
Suy ra .
Khi đó .
Ta có .
Vậy phép vị tự cần tìm là .
Lời giải
Ta có
.
Vậy .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.