Giải SBT Toán học 11 CTST Bài 3: Hai mặt phẳng vuông góc có đáp án

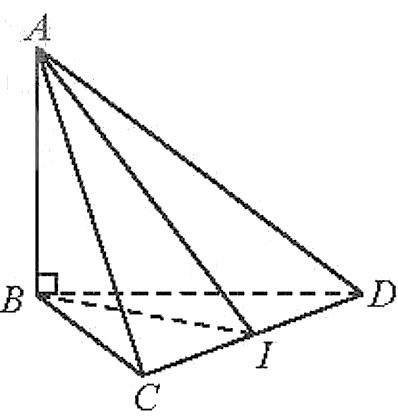
Gọi I là trung điểm của CD.

Ta có: CD ^ BI và CD ^ AB suy ra CD ^ AI.

Ta nhận thấy: CD là giao tuyến của 2 mặt phẳng (ACD) và (BCD);

Mà $\left\{\begin{array}{c}AI\perp CD,AI\subset \left(ACD\right)\\ BI\perp CD,BI\subset \left(BCD\right)\end{array}\right.$

Suy ra $\left(\right(ACD),(BCD\left)\right)=(AI,BI)=\widehat{AIB}.$

Tam giác BCD vuông cân tại B nên $BI=\frac{1}{2}CD=\frac{1}{2}.BC.\sqrt{2}=a.$

Xét tam giác ABI vuông tại B, ta có: $\tan \widehat{AIB}=\frac{AB}{BI}=\frac{1}{\sqrt{3}}\Rightarrow \widehat{AIB}=30°.$

Vậy góc giữa hai mặt phẳng (ACD) và (BCD) là $\widehat{AIB}=30°$

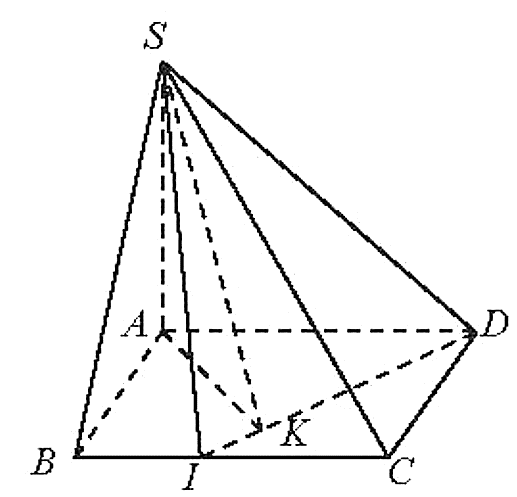
Vẽ AK ^ ID (K Î ID).

Ta có ID ^ SA và ID ^ AK (1)

Þ ID ^ (SAK) Þ ID ^ SK. (2)

Từ (1) và (2) suy ra $\left(\left(SDI\right),\left(ABCD\right)\right)=\widehat{AKS}=60°.$

Xét tam giác SAK vuông tại A có: $\sin \widehat{AKS}=\frac{SA}{SK}\Rightarrow SK=\frac{SA}{\sin 60°}=\frac{2a}{\sqrt{3}}$

Tam giác SAD vuông tại A, ta có: $SD=\sqrt{a^2+4a^2}=a\sqrt{5}$

Xét tam giác SID vuông tại S, ta có:

$\frac{1}{S{K}^2}=\frac{1}{S{I}^2}+\frac{1}{S{D}^2}\iff \frac{1}{S{I}^2}=\frac{1}{S{K}^2}-\frac{1}{S{D}^2}$

Do đó $SI=\frac{2a\sqrt{55}}{11}$

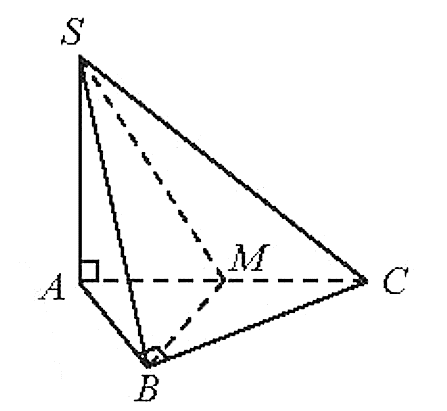
a) Ta có: BC ^ AB (giả thiết);

Đồng thời BC ^ SA (vì SA ^ (ABC)).

Þ BC ^ (SAB)

Þ (SBC) ^ (SAB).

b) Vì tam giác ABC là tam giác vuông cân tại B nên BM ^ AC.

Mà BM ^ SA (vì SA ^ (ABC))

Þ BM ^ (SAC) (1)

BM Ì (SBM) (2)

Từ (1) và (2) suy ra (SBM) ^ (SAC).

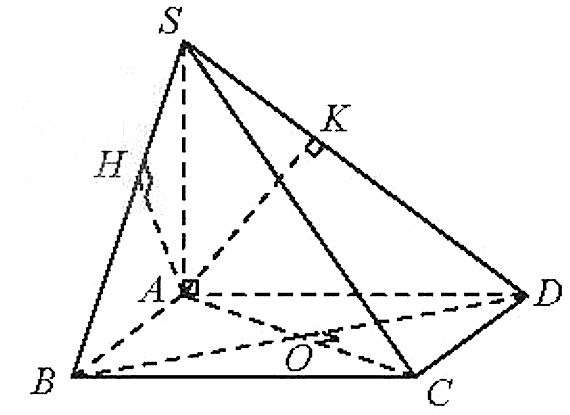
a) Theo giả thiết: 

$\left\{\begin{array}{l}\left(SAB\right)\perp \left(ABCD\right);\\ \left(SAD\right)\perp \left(ABCD\right);\\ \left(SAB\right)\cap \left(SAD\right)=SA.\end{array}\right.$

Suy ra SA ^ (ABCD).

Khi đó: $\left\{\begin{array}{l}BC\perp AB\left(ABCDlàhìnhvuông\right);\\ BC\perp SA(vìSA\perp \left(ABCD\right)).\end{array}\right.$

Þ BC ^ (SAB) Þ (SBC) ^ (SAB).

b) Theo giả thiết:

$\left\{\begin{array}{l}\left(SAB\right)\perp \left(ABCD\right);\\ \left(SAD\right)\perp \left(ABCD\right);\\ \left(SAB\right)\cap \left(SAD\right)=SA.\end{array}\right.$

Suy ra SA ^ (ABCD).

Khi đó: $\left\{\begin{array}{l}CD\perp AD\left(ABCDlàhìnhvuông\right);\\ CD\perp SA(vìSA\perp \left(ABCD\right)).\end{array}\right.$

Þ CD ^ (SAD) Þ (SCD) ^ (SAD).

c) Ta có: $\left\{\begin{array}{l}BD\perp AC\left(ABCDlàhìnhvuông\right);\\ BD\perp SA(vìSA\perp \left(ABCD\right)).\end{array}\right.$

Þ BD ^ (SAC) Þ (SBD) ^ (SAC).

d) Ta có:

(SAB) ^ (SBC) (Chứng minh trên);

(SAB) Ç (SBC) = SB;                           

Do đó AH ^ (SBC)

Mà AH ^ SB (giả thiết).

Nên AH ^ SC. (1)

Tương tự: AK ^ SC. (2)

Từ (1) và (2) suy ra: SC ^ (AHK).

Vậy (SAC) ^ (AHK).

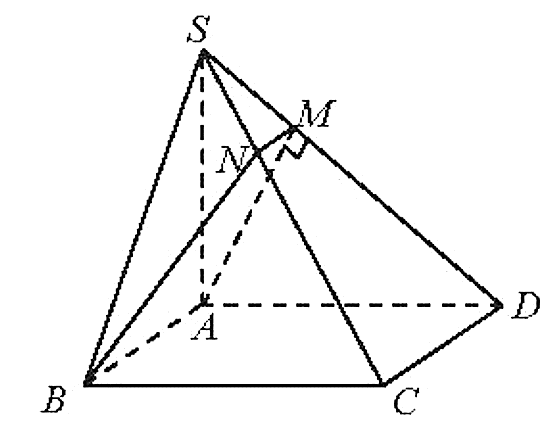
a) Ta có:

(SAB) ^ (ABCD);

(SAD) ^ (ABCD);         

Do đó SA ^ (ABCD).

(SAB) Ç (SAD) = SA.

Dễ dàng chứng minh được (SAD) ^ (SCD).

Vẽ AM ^ SD (M Î SD) Þ AM ^ (SCD)

Do đó (ABM) ^ (SCD) hay (ABM) là mặt phẳng (α) qua AB và vuông góc với mặt phẳng (SCD).

Trong mặt phẳng (SCD) kẻ MN // CD (N Î SC).

Suy ra: MN // AB Þ MN Ì (α).

Vậy các giao tuyến của (α) với các mặt của hình chóp là AB, BN, NM, MA.

b)

Ta có: MN // AB; AB ^ AM (vì AB ^ (SAD)).

Suy ra ABNM là hình thang vuông tại A và M.

Tam giác SAD vuông tại A có AM là đường cao nên:

$\frac{1}{A{M}^2}=\frac{1}{S{A}^2}+\frac{1}{A{D}^2}=\frac{1}{3a^2}+\frac{1}{a^2}=\frac{4}{3a^2}\Rightarrow AM=\frac{a\sqrt{3}}{2}.$

Vì MN // CD nên $\frac{MN}{CD}=\frac{SM}{SD}$

$\Rightarrow \frac{MN}{CD}=\frac{S{A}^2}{SD}\cdot \frac{1}{SD}=\frac{S{A}^2}{S{D}^2}=\frac{S{A}^2}{S{A}^2+A{D}^2}=\frac{3a^2}{4a^2}$

$\Rightarrow MN=\frac{3}{4}CD=\frac{3}{4}a$

 $\Rightarrow S_{ABMN}=\frac{1}{2}.AM.(MN+AB)=\frac{1}{2}.\frac{a\sqrt{3}}{2}.\left(\frac{3}{4}a+a\right)=\frac{7a^2\sqrt{3}}{16}$

Diện tích đáy lớn: S₁ = 2.2 = 4 m².

Diện tích đáy nhỏ: S₂ = 1.1 = 1m².

Giả sử các mặt bên có dạng như hình vẽ:

Dễ thấy: AH = 0.5 m Þ  $DH=\sqrt{A{D}^2-A{H}^2}=\frac{\sqrt{15}}{2}$

Diện tích các mặt bên: S₃ = $\frac{1}{2}.(AB+CD).DH=\frac{3\sqrt{15}}{4}$

Tổng diện tích các mặt cần sơn là:

S = S₁ + S₂ + 4.S₃ = 4 + 1 + 4.$\frac{3\sqrt{15}}{4}$ » 16,62 (m²).

Vậy tổng diện tích các bề mặt cần sơn khoảng 16,62 m².