Giải SGK Toán 11 CTST Tìm hiểu hàm số lượng giác bằng phần mềm GeoGebra có đáp án
27 người thi tuần này 4.6 780 lượt thi 5 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi giữa kì 1 Toán 11 năm 2026-2027 THPT Việt Đức (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 11 năm 2026-2027 THCS&THPT Tạ Quang Bửu (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 11 năm 2026-2027 THCS&THPT Nguyễn Bỉnh Khiêm (Hà Nội) có đáp án
Trắc nghiệm Công thức nhân xác suất cho hai biến cố độc lập lớp 11 (có đúng sai, trả lời ngắn)
Trắc nghiệm Công thức cộng xác suất lớp 11 (có đúng sai, trả lời ngắn)
Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Phùng Khắc Khoan (Thạch Thất-Hà Nội) có đáp án - mã đề 0123
Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Vạn Xuân (Hoài Đức-Hà Nội) có đáp án - Đề chẵn
Danh sách câu hỏi:
Câu 1/5
1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phiên bản online.
2. Các bước thao tác trên Geogebra: Nhập phương trình theo cú pháp y = sin(x) vào vùng nhập lệnh (Hình 2).
3. Ta có ngay đồ thị hàm số y = sin x trên vùng làm việc như Hình 3.
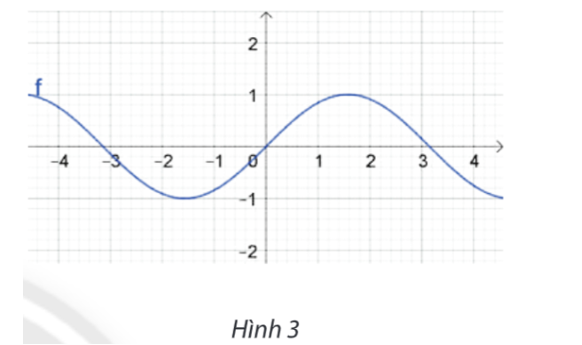
1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phiên bản online.
2. Các bước thao tác trên Geogebra: Nhập phương trình theo cú pháp y = sin(x) vào vùng nhập lệnh (Hình 2).
3. Ta có ngay đồ thị hàm số y = sin x trên vùng làm việc như Hình 3.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Học sinh thực hiện theo các bước ở hoạt động 1.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
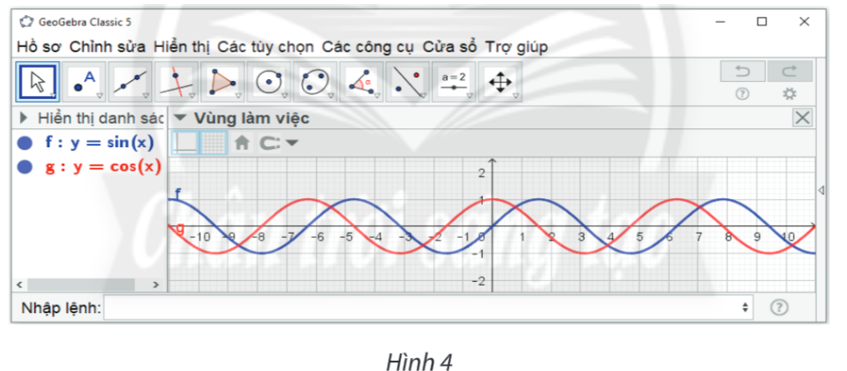
• Ta đã vẽ hàm số y = sin x trên hệ trục tọa độ ở hoạt động 1 (như hình vẽ).
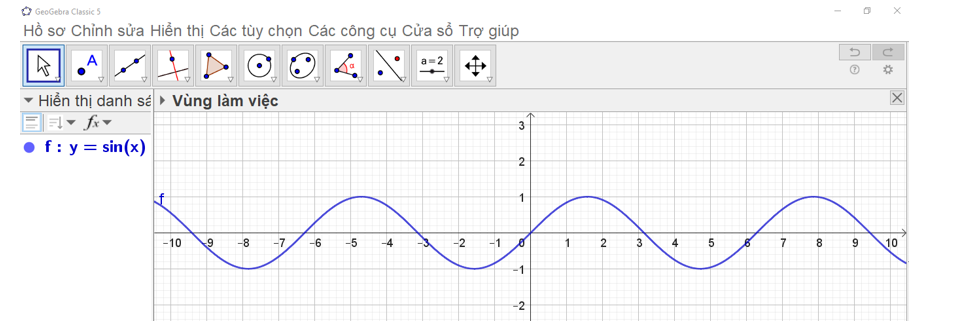
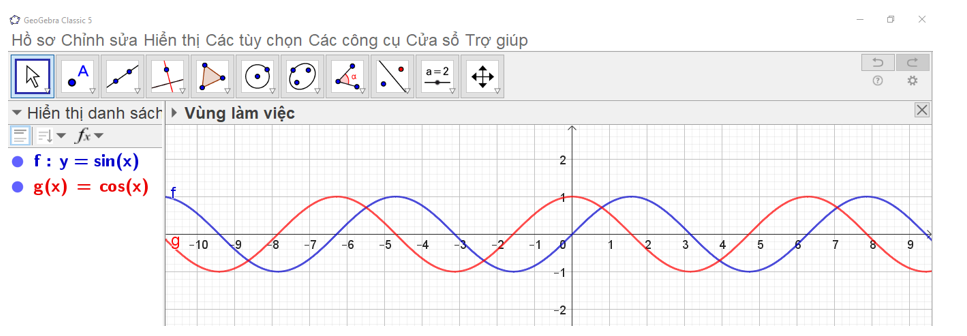
• Thao tác trên Geogebra: Nhập phương trình theo cú pháp y = cos(x) vào vùng nhập lệnh.
• Ta có ngay đồ thị hàm số y = cos x trên vùng làm việc như hình vẽ.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
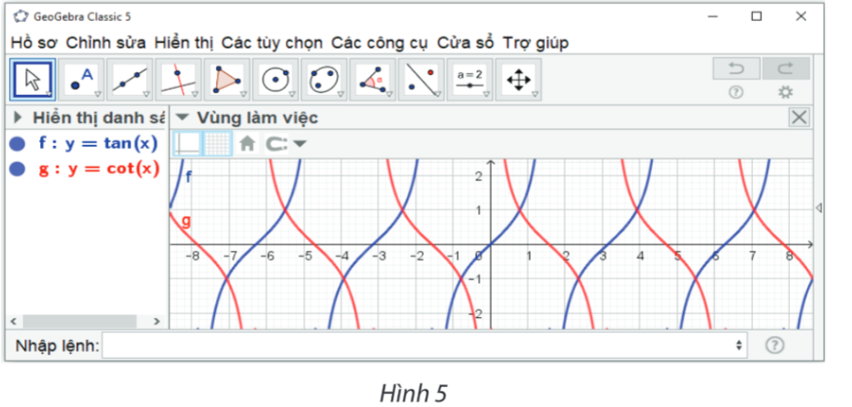
Ta thực hiện vẽ đồ thị hàm số lượng giác y = tan x và y = cot x trên cùng hệ trục tọa độ theo các bước sau:
Bước 1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phiên bản online.
Bước 2. Các bước thao tác trên Geogebra: Nhập phương trình theo cú pháp y = tan(x) vào vùng nhập lệnh (như hình vẽ).
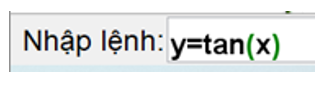
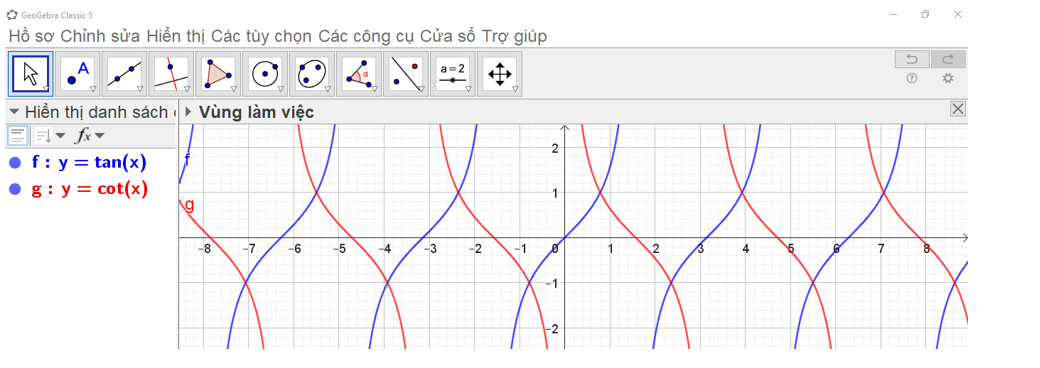
Ta có ngay đồ thị hàm số y = tan x trên vùng làm việc như hình vẽ.
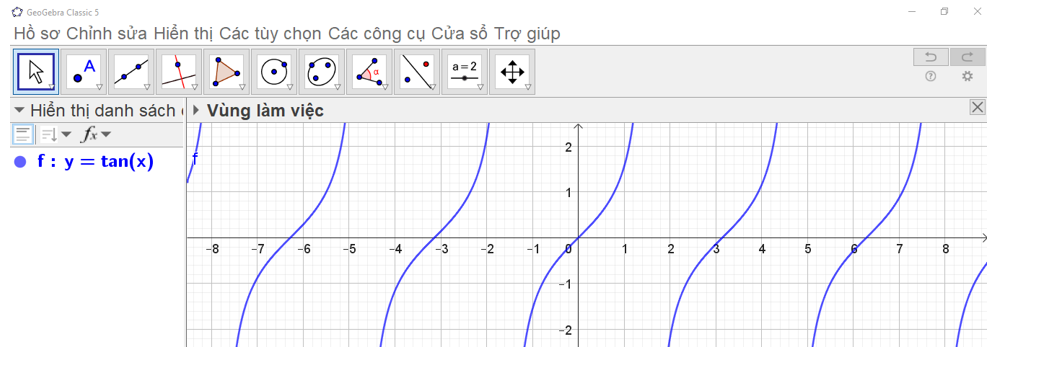
Bước 3. Các bước thao tác trên Geogebra: Nhập phương trình theo cú pháp y = cot(x) vào vùng nhập lệnh (như hình vẽ).
Ta có ngay đồ thị hàm số y = cot x trên vùng làm việc như hình vẽ.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
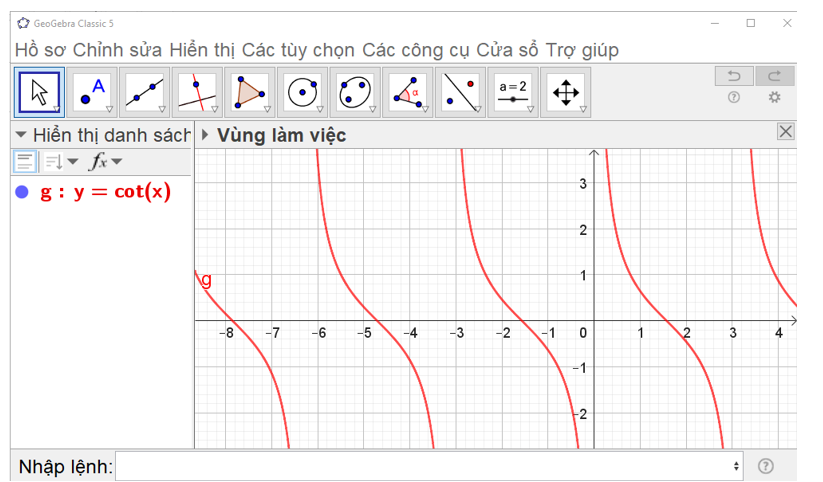
Dựa vào đồ thị hàm số y = cot x, ta có:
• Tập xác định: D = ℝ\{kπ | k ∈ ℤ}.
• Tập giá trị: ℝ.
• Tính chẵn lẻ: hàm số y = cot x là hàm số lẻ.
• Tính tuần hoàn: hàm số y = cot x là hàm tuần hoàn.
• Chu kì: T = π.
• Hàm số y = cot x không có khoảng đồng biến.
• Hàm số y = cot x nghịch biến trên (kπ; π + kπ) (k ∈ ℤ).
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập