Giải SBT Toán học 11 CTST Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện có đáp án
41 người thi tuần này 4.6 458 lượt thi 4 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
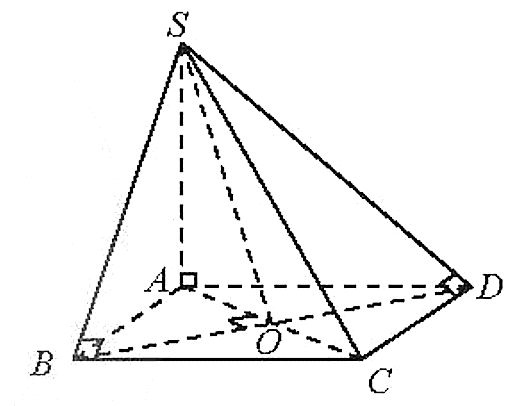
a) Ta có:
Suy raAB là hình chiếu của SB trên (ABCD).
Do đó (SB, (ABCD)) = (SB, AB).
Trong tam giác SAB vuông tại A, ta có:
Vậy
b) Tương tự câu a) ta xác định được (SC, (ABCD)) = (SC, AC).
Trong tam giác SAC vuông tại A, ta có:
Vậy
c) Tương tự câu a) ta xác định được (SD, (ABCD)) = (SD,AD).
Trong tam giác SAD vuông tại A, ta có:
Vậy
d) Ta có:
Þ BD ^ (SAC) hay BO ^ (SAC). (1)
Mà SB Ç (SAC) = S. (2)
Từ (1) và (2) suy ra SO là hình chiếu của SB trên (SAC).
Do đó: (SB, (SAC)) = (SB, SO).
Trong tam giác SBO vuông tại O, ta có:
Vậy
Lời giải
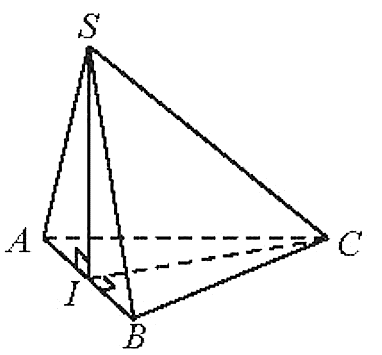
a) Vì AI là hình chiếu của SA trên (ABC).
Do đó (SA, (ABC)) = (SA, AI).
Vì tam giác SAI vuông cân tại I
Vậy
b) Ta có tam giác ABC đều nên CI ^ AB,
Ta có:
Mà SC Ç (SAB) = S. (2)
Từ (1) và (2) Þ SI là hình chiếu của SC trên (SAB).
Do đó (SC, (SAB)) = (SC, SI).
Trong tam giác SAB vuông tại S,
Trong tam giác SCI vuông tại I, ta có
Vậy
Lời giải
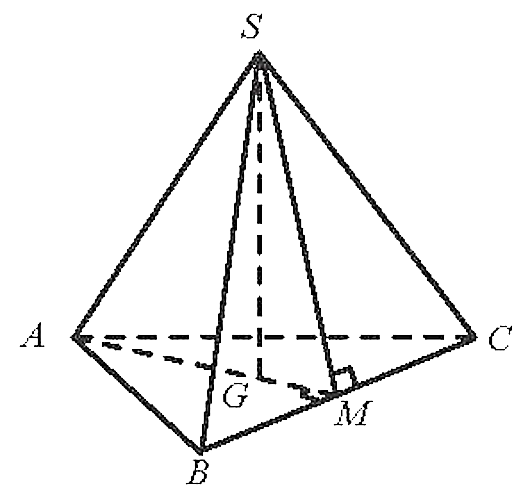
Gọi M là trung điểm BC, G là trọng tâm tam giác ABC.
Ta có SG ^ (ABC), SM ^ BC, AM ^ BC.
Suy ra là góc phẳng nhị diện [S, BC, A].
Ta tính được
Þ GM = SG.
Ta có tam giác SMG vuông cân tại G, suy ra số đo góc phẳng nhị diện [S, BC, A] =
Lời giải
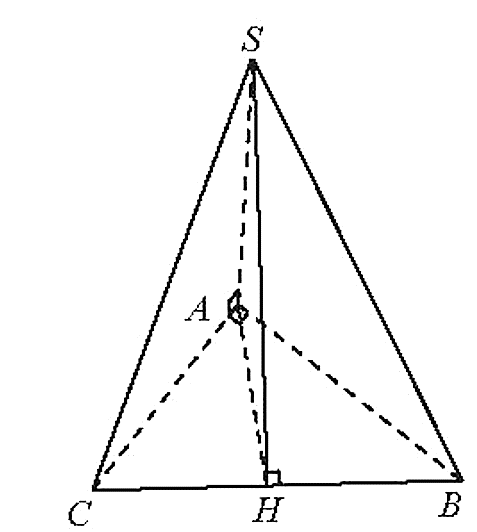
Vẽ AH ^ BC (H Î BC), ta có SH ^ BC.
Suy ra là góc phẳng nhị diện [S, BC, A].
Ta có AH = AC.sin60° = = SA
Do đó = 45°.